黄金長方形

黄金長方形と、黄金長方形内の正方形の列と黄金螺旋

黄金長方形（おうごんちょうほうけい、英: golden rectangle）とは、縦横の長さの比が黄金比、すなわち

$1:{\frac {1+{\sqrt {5}}}{2}}\approx 1.618$

の長方形のことである。

黄金長方形は、自己相似性などの特徴的な性質を示すことで知られており、日本で用いられる名刺はこの長方形に近い形状をしている。

性質

自己相似性と黄金螺旋

黄金長方形と黄金螺旋。

一辺の長さがフィボナッチ数の正方形を貼り合わせてできる長方形の形は、黄金長方形に収束する。

黄金長方形は自己相似性を持ち、黄金長方形から最大の正方形を除く（もしくは加える）と、残った長方形は元の黄金長方形と相似になる。これを繰り返すと、無数の自己相似な図形が出来ていく。

図のように、正方形の列において角の点を滑らかにつないでいくと、渦巻が出来ていく。この渦巻は、巻貝の貝殻などに見られる対数螺旋の一種であり、黄金螺旋と呼ばれる。黄金螺旋は、90度の回転毎にφ倍拡大（縮小）されるため、式では以下のように表される。

$r=\left(\varphi ^{\frac {2}{\pi }}\right)^{\theta }$

逆に、内側からフィボナッチ数列を一辺の長さとする正方形を連ねていくと、次第に黄金長方形に近くなる。

黄金長方形の左上の角の点を点(0, 0)とし、長辺の長さをφ、短辺の長さを1とするとき、螺旋の中心の座標(x₀, y₀)は、以下のようになる。

$x_{0}=\sum _{n=0}^{\infty }\left({\frac {1}{\varphi ^{4n}}}+{\frac {1}{\varphi ^{4n+1}}}-{\frac {1}{\varphi ^{4n+2}}}-{\frac {1}{\varphi ^{4n+3}}}\right)$

$={\frac {2\varphi +1}{\varphi +2}}={\frac {5+3{\sqrt {5}}}{10}}\approx 1.17082$

$y_{0}=\sum _{n=0}^{\infty }\left(-{\frac {1}{\varphi ^{4n}}}+{\frac {1}{\varphi ^{4n+1}}}+{\frac {1}{\varphi ^{4n+2}}}-{\frac {1}{\varphi ^{4n+3}}}\right)$

$=-{\frac {1}{2+\varphi }}={\frac {{\sqrt {5}}-5}{10}}\approx -0.276393$

渦巻き

黄金長方形と渦巻き。

黄金長方形の短辺を斜辺ではない長辺とする、斜辺ではない短辺との比率が2:1である四つの合同な直角三角形を、黄金長方形の内部に配置するができる。これを無数に繰り返すことで、一回の繰り返しごとにφ倍小さくなり、arctan1/2回転する、無数の自己相似な長方形を描くことができ、直角三角形の角の点を結べば渦巻きを描くことができる。

無数の直角三角形の角を結んでできる螺旋は、ピッチが$\theta ={\frac {\ln {\varphi }}{\arctan {\frac {1}{2}}}}\approx 1.038=59.47^{\circ }$である。

向かい合う二つの直角三角形に囲まれた平行四辺形のうち、菱形である平行四辺形（灰色の直角三角形に囲まれた平行四辺形）は、直行する黄金比φの対角線を持つため、黄金菱形である。

はじめの直角三角形の斜辺ではない長辺と短辺の長さがそれぞれ1と2であるとき、各螺旋の長さは$\varphi ^{2}=\sum _{n=0}^{\infty }\varphi ^{-n}$であり、各螺旋に囲まれた無数の直角三角形の面積は$\varphi =\sum _{n=0}^{\infty }\varphi ^{-2n}$となる。また、図の灰色の部分の周の長さは$2{\sqrt {5}}\varphi =5+{\sqrt {5}}$であり、黄色の部分の周の長さは$4\varphi =2+2{\sqrt {5}}$である。

正多角形と多面体

ユークリッドは、三つの合同な円に内接する三つの正多角形、正五角形、正六角形、および正十角形を用いて黄金長方形を作図する方法を示した。これら三つの図形の辺の長さa, b, cはa² = b² + c²を満たすため、ピタゴラスの定理の逆より、囲まれた図形は直角三角形となる。そして、半径が等しい正六角形と正十角形の辺の比は黄金比φであるため、この直角三角形は黄金長方形を半分に分割したものとなり、これを用いて黄金長方形を作図することができる。

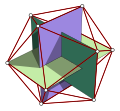
正二十面体の向かい合う二辺の凸包は黄金長方形を形成し、正二十面体の十二弧の頂点は、ボロミアン環のパターンで三つの黄金長方形に分解することができる。

• 
  三つの正多角形と黄金長方形。
• 
  正二十面体と黄金長方形。

作図

黄金長方形の作図。

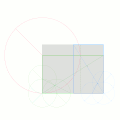
ピタゴラスの定理より、$\left({\frac {1}{2}}\right)^{2}+1^{2}=\left({\frac {\sqrt {5}}{2}}\right)^{2}$なので、正方形の半分の四角形の対角線は、正方形に加えた小さな黄金長方形の二点を通る円の半径に等しい。したがって、黄金長方形は定規とコンパスによる作図が可能である。

1. 正方形を描く
2. 正方形の一辺の中点から、向かい合う点へ線を引く
3. 引いた線を半径として用いて、弧を描く
4. 2.で用いた辺を弧と交わるまで延長すれば、黄金長方形の長辺ができる

ギャラリー

• 
  黄金長方形では、(長辺 - 短辺) : 短辺 = 短辺 : 長辺 が成り立つことを表した図。
• 
  黄金長方形から最大正方形を切り取っていった図（残った長方形も黄金長方形になる）。
• 
  黄金数 φ について、φ(φ − 1) = 1 を、面積で表した図。青線が、縦横の長さ 1, φ の黄金長方形2個を表し、右上の赤網目部分が φ(φ − 1)、左下の赤網目部分が 1 を表す。
• 
  黄金数 φ について、φ(φ − 1) = 1 を、面積で表した図。縦横の長さが 1, φ の黄金長方形（青線）において、斜線部分が等積となる。また、赤網目部分は √5φ = 1 + φ² を表している。
• 
  互いに合同な直角二等辺三角形を図のように並べると黄金長方形が出来る。
• 
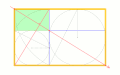
  正円とその中心を通る水平並びに傾き２の直線との交点を活用すると図のように黄金長方形（赤・青・緑）を描ける。
• 
  幾何学的に或る長方形（灰色）からその長辺または短辺の全長を使い切った黄金長方形を切り取る方法の一例。（青枠または緑枠で示される長方形が黄金長方形となっている。）
• 
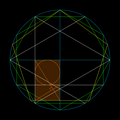
  「半径２の正円」（緑）と「辺の長さが１とφの黄金長方形」（橙）を活用すると図のように当該正円の円周を２０等分する点を求めることができる。
• 
  同一の正円(青)に内接する正五角形(黄)と正六角形(緑)を活用して黄金長方形(橙)を作り出す例

関連項目

• 黄金比
• 対数螺旋
• フィボナッチ数
• 黄金三角形
• 黄金菱形