直交対角線四角形
表示
この記事は英語版の対応するページを翻訳することにより充実させることができます。(2020年12月) 翻訳前に重要な指示を読むには右にある[表示]をクリックしてください。
|
このページ名「直交対角線四角形」は暫定的なものです。(2023年2月) |

直交対角線四角形(ちょっこうたいかくせんしかっけい、英: Orthodiagonal quadrilateral)とは、対角線が直交している四角形である[1]。
概要
[編集]直交対角線四角形においては、向かい合う辺の長さの2乗の合計はもう一方の向かい合う辺の長さの2乗の合計と等しくなる[2][3]。
これは、ピタゴラスの定理からいえることである。これはまた、余弦定理、空間ベクトル、背理法、複素数の使用など、さまざまな方法で証明できる[4]。
別の特徴付けによると、凸四角形ABCDの対角線が直交することは、次の式が成り立つことに同値である。ただしPは対角線の交点である。
この等式は、Pの四角形の各辺への射影が共円四角形の頂点となることとも同値である[4]。
また、凸四角形の対角線が直交することは、そのヴァリニョンの平行四辺形(四角形の辺の中点を結んでできる平行四辺形)が長方形であることに同値である[4]。
面積
[編集]直交対角線四角形の面積Kは、対角線pとqの長さの積の半分で求められる[5]。
逆に、この式で面積を計算できる凸四角形は、対角線が直交している[4]。
画像
[編集]-
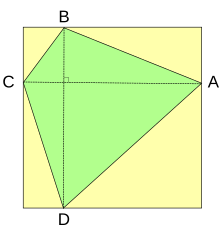
四角形は直交対角線四角形である。及びは四角形に内接する長方形である。
-
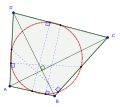
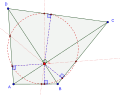
4つの中点は同一円周上にある。さらに、中点から対辺に下ろした垂線の足もこの円周上にある。
-
対角線の交点から各辺に下ろした垂線の足は、同一円周上にある。さらに、各垂線が対辺と交わる点もこの円周上にある。
-
台形かつ直交対角線四角形
-
凹四角形かつ直交対角線四角形
-
凧形は直交対角線四角形の特殊な場合である。
脚注
[編集]- ^ Berliner Mathematische Gesellschaft (1907) (German). Archiv der Mathematik und Physik. unknown library. B. G. Teubner
- ^ Altshiller-Court, N. (2007), College Geometry, Dover Publications. Republication of second edition, 1952, Barnes & Noble, pp. 136-138.
- ^ Mitchell, Douglas, W. (2009), “The area of a quadrilateral”, The Mathematical Gazette 93 (July): 306–309.
- ^ a b c d Josefsson, Martin (2012), “Characterizations of Orthodiagonal Quadrilaterals”, Forum Geometricorum 12: 13–25
- ^ Harries, J. (2002), “Area of a quadrilateral”, The Mathematical Gazette 86 (July): 310–311