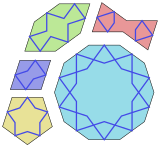
十芒星
表示
| Regular decagram | |
|---|---|
 A regular decagram | |
| 種類 | 星型正多角形 |
| 辺・頂点 | 10 |
| シュレーフリ記号 | {10/3} t{5/3} |
| コクセター図形 | |
| 対称性群 | 二面体 (D10) |
| 内角 (度) | 72° |
| 双対多角形 | 自己双対 |
| 要素 | 星型、円型、等辺、等角、同辺 |
幾何学において、十芒星(英語: decagram、デカグラム)は、10個の角を持つ星型多角形。正十芒星は、正十角形の頂点を3つおきに結んでいくとできる図形である。シュレーフリ記号は{10/3}である[1]。
正十芒星
[編集]1辺が1である正十芒星の場合、各辺を交点で区切った長さの割合は以下のようになる。
応用
[編集]正十芒星は、ギリータイルの装飾図柄の1つとして用いられている[2]。
関連図形
[編集]正十芒星は、正十角形と同じ頂点を持つ、記号 {10/n} で表される10点ポリグラムである。このポリグラムのうち、{10/3} (3点おきに結んだもの)のみが星型正十角形を形成するが、星型正多角形が組み合わさったものと解釈できるものは3つある。
| 形状 | 凸 | 組み合わせ | 星型多角形 | 組み合わせ | |
|---|---|---|---|---|---|
| 図 | 
|

|

|

|
|
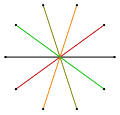
| 記号 | {10/1} = {10} | {10/2} = 2{5} | {10/3} | {10/4} = 2{5/2} | {10/5} = 5{2} |
{10/2} は、3次元の複合十二面体二十面体、4次元の複合百二十胞体六百胞体の2次元のものと見ることができる。つまり、それぞれの双対にある2つの五角形ポリソープを組み合わせたものである。
{10/4}も同様の理由により、3次元における小星型十二面体と大十二面体を組み合わせたもの、大二十面体と大星型十二面体を組み合わせたものと2次元において等価なものとみなすことができる。4次元においては相当するものは6つあり、そのうち2つは五芒星自身のように2つの自己双対星ポリトープを組み合わせたもの、複合大百二十胞体、複合大星型百二十胞体である。複合多面体の一覧参照。
正五角形と五芒星の先端を大きく切り取ると、10個の等間隔にうたれた頂点と2辺の長さが頂点推移のままである(図形の対称性により任意の2頂点を互いに変換できる)中間星型多角形ができる[5][6][7]。
| 正多角形・正星型多角形 | 等角 | 正多角形・正星型多角形 二重被覆 | |
|---|---|---|---|
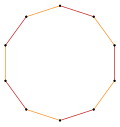 t{5} = {10} |
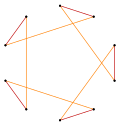
|

|
 t{5/4} = {10/4} = 2{5/2} |
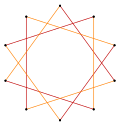 t{5/3} = {10/3} |

|
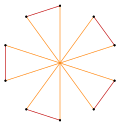
|
 t{5/2} = {10/2} = 2{5} |
脚注
[編集]- ^ Barnes, John (2012), Gems of Geometry, Springer, pp. 28–29, ISBN 9783642309649
- ^ Sarhangi, Reza (2012), “Polyhedral Modularity in a Special Class of Decagram Based Interlocking Star Polygons”, Bridges 2012: Mathematics, Music, Art, Architecture, Culture, pp. 165–174.
- ^ Regular polytopes, p 93-95, regular star polygons, regular star compounds
- ^ Coxeter, Introduction to Geometry, second edition, 2.8 Star polygons p.36-38
- ^ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum.
- ^ Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954). “Uniform polyhedra”. Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences (The Royal Society) 246 (916): 411. Bibcode: 1954RSPTA.246..401C. doi:10.1098/rsta.1954.0003. ISSN 0080-4614. JSTOR 91532. MR0062446.
- ^ Coxeter, The Densities of the Regular polytopes I, p.43 If d is odd, the truncation of the polygon {p/q} is naturally {2n/d}. But if not, it consists of two coincident {n/(d/2)}'s; two, because each side arises from an original side and once from an original vertex. Thus the density of a polygon is unaltered by truncation.