出典: フリー百科事典『ウィキペディア(Wikipedia)』
ロジスティック
確率密度関数 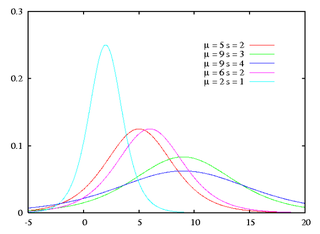 |
累積分布関数 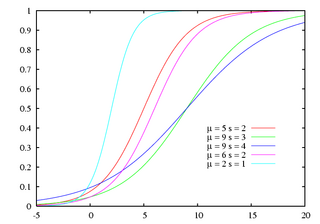 |
| 母数 |
 :位置母数(英語版)(実数) :位置母数(英語版)(実数)
 :尺度母数(英語版)(実数) :尺度母数(英語版)(実数) |
|---|
| 台 |
 |
|---|
| 確率密度関数 |
 |
|---|
| 累積分布関数 |
 |
|---|
| 期待値 |
 |
|---|
| 中央値 |
 |
|---|
| 最頻値 |
 |
|---|
| 分散 |
 |
|---|
| 歪度 |
 |
|---|
| 尖度 |
 |
|---|
| エントロピー |
 |
|---|
| モーメント母関数 |
 の場合、 の場合、

ここで、 はベータ関数 はベータ関数 |
|---|
| 特性関数 |
 の場合、 の場合、
 |
|---|
| テンプレートを表示 |
ロジスティック分布(ロジスティックぶんぷ、英: logistic distribution)は、連続確率分布の一つで、その累積分布関数がロジスティック関数であるものである。正規分布と同様に対称なS字(シグモイド)型の累積分布関数、釣鐘型の確率密度関数を持ち一見して両者は類似しているが、ロジスティック分布の方が裾が長く密度関数は平均から離れても下がりにくい。
確率変数を実数 x (−∞ < x < ∞) とするときのロジスティック分布は、
累積分布関数  が
が

あるいは、
確率密度関数  が
が

となる分布として定義される。
このとき、期待値は μ、分散は  である。
歪度は 0 で正規分布と同様に平均のまわりで対称であるが、尖度は 6/5 = 1.2 となる。
である。
歪度は 0 で正規分布と同様に平均のまわりで対称であるが、尖度は 6/5 = 1.2 となる。
- 蓑谷千凰彦、統計分布ハンドブック、朝倉書店 (2003).
- B. S. Everitt(清水良一訳)、統計科学辞典, 朝倉書店 (2002).
|
|---|
離散単変量で
有限台 | |
|---|
離散単変量で
無限台 | |
|---|
連続単変量で
有界区間に台を持つ | |
|---|
連続単変量で
半無限区間に台を持つ | |
|---|
連続単変量で
実数直線全体に台を持つ | |
|---|
連続単変量で
タイプの変わる台を持つ | |
|---|
| 混連続-離散単変量 | |
|---|
| 多変量 (結合) | |
|---|
| 方向 | |
|---|
| 退化と特異 | |
|---|
| 族 | |
|---|
| サンプリング法(英語版) | |
|---|
|
|





















