出典: フリー百科事典『ウィキペディア(Wikipedia)』
非心t 分布 (ひしんティーぶんぷ、英 : noncentric t-distribution )とは、確率分布 と統計学 におけるスチューデントのt分布 を一般化したものである。
非心な統計母数 、例えば「X の上位10パーセント値」のようなものの信頼区間 を標本データだけに基いて計算するのに有用である。
Z は分散 1 、平均 0 の正規分布 に従う確率変数 、V は自由度 νのカイ二乗分布 に従いかつ、Z と独立な確率変数、μは実定数としたときに、
T
=
Z
+
μ
V
/
ν
{\displaystyle T={\frac {Z+\mu }{\sqrt {V/\nu }}}}
が従う分布のことを「自由度ν、非心パラメーターμの非心t分布」と呼ぶ。μ=0の場合はt分布 そのものである。この非心t分布においては(非心F分布 (英語版 )
この非心t分布の累積分布関数 は、以下の式で与えられる。[ 1]
F
ν
,
μ
(
x
)
=
{
F
~
ν
,
μ
(
x
)
,
if
x
≥
0
;
1
−
F
~
ν
,
−
μ
(
x
)
,
if
x
<
0
,
{\displaystyle F_{\nu ,\mu }(x)={\begin{cases}{\tilde {F}}_{\nu ,\mu }(x),&{\mbox{if }}x\geq 0;\\1-{\tilde {F}}_{\nu ,-\mu }(x),&{\mbox{if }}x<0,\end{cases}}}
ここで、
F
~
ν
,
μ
(
x
)
=
Φ
(
−
μ
)
+
1
2
∑
j
=
0
∞
[
p
j
I
y
(
j
+
1
2
,
ν
2
)
+
q
j
I
y
(
j
+
1
,
ν
2
)
]
,
{\displaystyle {\tilde {F}}_{\nu ,\mu }(x)=\Phi (-\mu )+{\frac {1}{2}}\sum _{j=0}^{\infty }\left[p_{j}I_{y}\left(j+{\frac {1}{2}},{\frac {\nu }{2}}\right)+q_{j}I_{y}\left(j+1,{\frac {\nu }{2}}\right)\right],}
I
y
(
a
,
b
)
{\displaystyle I_{y}\,\!(a,b)}
不完全ベータ関数 ,
y
=
x
2
x
2
+
ν
,
{\displaystyle y={\frac {x^{2}}{x^{2}+\nu }},}
p
j
=
1
j
!
exp
{
−
μ
2
2
}
(
μ
2
2
)
j
,
{\displaystyle p_{j}={\frac {1}{j!}}\exp \left\{-{\frac {\mu ^{2}}{2}}\right\}\left({\frac {\mu ^{2}}{2}}\right)^{j},}
q
j
=
μ
2
Γ
(
j
+
3
/
2
)
exp
{
−
μ
2
2
}
(
μ
2
2
)
j
,
{\displaystyle q_{j}={\frac {\mu }{{\sqrt {2}}\Gamma (j+3/2)}}\exp \left\{-{\frac {\mu ^{2}}{2}}\right\}\left({\frac {\mu ^{2}}{2}}\right)^{j},}
であり、Φ は標準正規分布の累積分布関数 である。
他の表現として、以下の書き方もできる。
F
v
,
μ
(
x
)
=
{
1
2
∑
j
=
0
∞
1
j
!
(
−
μ
2
)
j
e
−
μ
2
2
Γ
(
j
+
1
2
)
π
I
(
v
v
+
x
2
;
v
2
,
j
+
1
2
)
,
x
≥
0
1
−
1
2
∑
j
=
0
∞
1
j
!
(
−
μ
2
)
j
e
−
μ
2
2
Γ
(
j
+
1
2
)
π
I
(
v
v
+
x
2
;
v
2
,
j
+
1
2
)
,
x
<
0
{\displaystyle F_{v,\mu }(x)={\begin{cases}{\frac {1}{2}}\sum _{j=0}^{\infty }{\frac {1}{j!}}(-\mu {\sqrt {2}})^{j}e^{\frac {-\mu ^{2}}{2}}{\frac {\Gamma ({\frac {j+1}{2}})}{\sqrt {\pi }}}I\left({\frac {v}{v+x^{2}}};{\frac {v}{2}},{\frac {j+1}{2}}\right),&x\geq 0\\1-{\frac {1}{2}}\sum _{j=0}^{\infty }{\frac {1}{j!}}(-\mu {\sqrt {2}})^{j}e^{\frac {-\mu ^{2}}{2}}{\frac {\Gamma ({\frac {j+1}{2}})}{\sqrt {\pi }}}I\left({\frac {v}{v+x^{2}}};{\frac {v}{2}},{\frac {j+1}{2}}\right),&x<0\end{cases}}}
ここで、Γ は ガンマ関数 、I は、正則化された不完全ベータ関数 である。
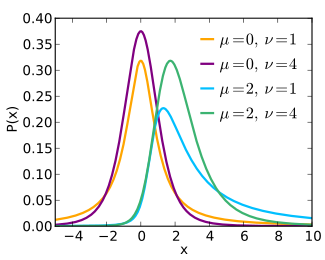
この非心t分布の確率密度関数 は[ 2]
f
(
t
)
=
ν
ν
/
2
e
−
ν
μ
2
/
2
(
t
2
+
ν
)
π
Γ
(
ν
/
2
)
2
(
ν
−
1
)
/
2
(
t
2
+
ν
)
(
ν
+
1
)
/
2
{\displaystyle f(t)={\frac {\nu ^{\nu /2}e^{-\nu \mu ^{2}/2(t^{2}+\nu )}}{{\sqrt {\pi }}\Gamma (\nu /2)2^{(\nu -1)/2}(t^{2}+\nu )^{(\nu +1)/2}}}}
×
∫
0
∞
x
ν
exp
[
−
1
2
(
x
−
μ
t
t
2
+
ν
)
2
]
d
x
{\displaystyle \times \int _{0}^{\infty }x^{\nu }\exp \left[-{\frac {1}{2}}\left(x-{\frac {\mu t}{\sqrt {t^{2}+\nu }}}\right)^{2}\right]\,dx}
ここで ν > 0実数 である。
非心t分布の平均および分散は[ 3]
E
[
T
]
=
{
μ
ν
2
Γ
(
(
ν
−
1
)
/
2
)
Γ
(
ν
/
2
)
ν
>
1
Does not exist
ν
≤
1
{\displaystyle \operatorname {E} \left[T\right]={\begin{cases}\mu {\sqrt {\frac {\nu }{2}}}{\frac {\Gamma ((\nu -1)/2)}{\Gamma (\nu /2)}}&\nu >1\\{\mbox{Does not exist}}&\nu \leq 1\end{cases}}}
Var
[
T
]
=
{
ν
(
1
+
μ
2
)
ν
−
2
−
μ
2
ν
2
(
Γ
(
(
ν
−
1
)
/
2
)
Γ
(
ν
/
2
)
)
2
ν
>
2
Does not exist
ν
≤
2
.
{\displaystyle \operatorname {Var} \left[T\right]={\begin{cases}{\frac {\nu (1+\mu ^{2})}{\nu -2}}-{\frac {\mu ^{2}\nu }{2}}\left({\frac {\Gamma ((\nu -1)/2)}{\Gamma (\nu /2)}}\right)^{2}&\nu >2\\{\mbox{Does not exist}}&\nu \leq 2\end{cases}}.}
もしも μ = 0t分布 になる。
もしも T が非心t分布にしたがう場合、Z = T 2 Z は非心F分布 (英語版 )
T が非心t分布にしたがう場合、
Z
=
lim
ν
→
∞
T
{\displaystyle Z=\lim _{\nu \to \infty }T}
Z は正規分布 にしたがう。本記事は英語版ウィキペディア記事
Noncentral chi-square_distribution. [:en] Wikipedia: Free Encyclopedia (English language), 14:14, 21 July 2007 からの抄訳に基づいて作成された。
離散単変量で 離散単変量で 連続単変量で 連続単変量で 連続単変量で 連続単変量で 混連続-離散単変量 多変量 (結合) 方向 退化 と特異 族 サンプリング法 (英語版 )






![{\displaystyle {\tilde {F}}_{\nu ,\mu }(x)=\Phi (-\mu )+{\frac {1}{2}}\sum _{j=0}^{\infty }\left[p_{j}I_{y}\left(j+{\frac {1}{2}},{\frac {\nu }{2}}\right)+q_{j}I_{y}\left(j+1,{\frac {\nu }{2}}\right)\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd7972cec4038f87c7260ec14df8ec820506d215)






![{\displaystyle \times \int _{0}^{\infty }x^{\nu }\exp \left[-{\frac {1}{2}}\left(x-{\frac {\mu t}{\sqrt {t^{2}+\nu }}}\right)^{2}\right]\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d797e16d044cf717a1a9c67eb92847e560a160f4)
![{\displaystyle \operatorname {E} \left[T\right]={\begin{cases}\mu {\sqrt {\frac {\nu }{2}}}{\frac {\Gamma ((\nu -1)/2)}{\Gamma (\nu /2)}}&\nu >1\\{\mbox{Does not exist}}&\nu \leq 1\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f037dd6350b54195f80c1af6443b0c8527c88cdc)
![{\displaystyle \operatorname {Var} \left[T\right]={\begin{cases}{\frac {\nu (1+\mu ^{2})}{\nu -2}}-{\frac {\mu ^{2}\nu }{2}}\left({\frac {\Gamma ((\nu -1)/2)}{\Gamma (\nu /2)}}\right)^{2}&\nu >2\\{\mbox{Does not exist}}&\nu \leq 2\end{cases}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb194e9655efe8a55f84d3deb0c5846913286708)
