原文と比べた結果、この記事には多数の(または内容の大部分に影響ある)誤訳 があることが判明しています。情報の利用には注意してください。 正確な表現に改訳できる方を求めています。
数学では、ホモロジー代数 の Ext関手 (Ext functors)は、Hom関手 の導来関手 であり、Tor関手 と同様、ホモロジー代数学 の中心概念である。ホモロジー代数学では、代数的トポロジー のアイデアが代数的構造 の不変量 を定義するのに使われている。群のコホモロジー やリー環 、結合多元環 はすべてExtの言葉で定義できる。Extという名称は、最初のExt群Ext1 により加群 の拡大 が分類できることから来ている。
Ext関手は、最初代数幾何学 で使われ、その後は数学の多くの分野で共通して使われている。名称の "Ext" は、関手 とアーベル圏 での拡大(Extension)との関係からきている。
R を環 とし、ModR R の上の加群 の圏 とする。B を ModR R A に対し T (B ) = HomR A ,B ) とする。これは左完全関手 であるので、右導来関手 Rn T を持っている。Ext関手は、
Ext
R
n
(
A
,
B
)
=
(
R
n
T
)
(
B
)
{\displaystyle \operatorname {Ext} _{R}^{n}(A,B)=(R^{n}T)(B)}
により定義される。これは入射分解 [ 1]
0
→
B
→
I
0
→
I
1
→
…
{\displaystyle 0\rightarrow B\rightarrow I^{0}\rightarrow I^{1}\rightarrow \dots }
を適当にとり、
0
→
Hom
R
(
A
,
I
0
)
→
Hom
R
(
A
,
I
1
)
→
…
.
{\displaystyle 0\rightarrow \operatorname {Hom} _{R}(A,I^{0})\rightarrow \operatorname {Hom} _{R}(A,I^{1})\rightarrow \dots .}
を計算することにより得ることができる。従って、(R n T )(B ) はこの複体のホモロジー である。HomR A ,B ) は複体から除外されることに注意する。
もうひとつの別な定義は、関手 G (A )=HomR A ,B ) を使って定義される。固定された加群 B に対し、これは反変 な左完全関手 であり、よって、右導来関手 Rn G を持ち、
Ext
R
n
(
A
,
B
)
=
(
R
n
G
)
(
A
)
{\displaystyle \operatorname {Ext} _{R}^{n}(A,B)=(R^{n}G)(A)}
を定義することができる。
Ext関手は、適当な射影分解
⋯
→
P
1
→
P
0
→
A
→
0
,
{\displaystyle \dots \rightarrow P^{1}\rightarrow P^{0}\rightarrow A\rightarrow 0,}
を選択し、双対な計算
0
→
Hom
R
(
P
0
,
B
)
→
Hom
R
(
P
1
,
B
)
→
…
{\displaystyle 0\rightarrow \operatorname {Hom} _{R}(P^{0},B)\rightarrow \operatorname {Hom} _{R}(P^{1},B)\rightarrow \dots }
を実行することによっても得られる。このとき、(Rn G )(A ) はこの複体のホモロジーである。再び、HomR A ,B ) が複体から除外されることに注意する。
これらの 2つの構成は、同型 となることが分かり、よって両方とも Ext関手の計算に使うことができる。
Ext関手の命名は、加群の拡大(extension)との関係で命名された。R -加群 A と B が与えられると、A の B による拡大 は、R-加群の短完全系列
0
→
B
→
E
→
A
→
0
{\displaystyle 0\rightarrow B\rightarrow E\rightarrow A\rightarrow 0}
である。2つの拡大
0
→
B
→
E
→
A
→
0
{\displaystyle 0\rightarrow B\rightarrow E\rightarrow A\rightarrow 0}
0
→
B
→
E
′
→
A
→
0
{\displaystyle 0\rightarrow B\rightarrow E^{\prime }\rightarrow A\rightarrow 0}
は、次の可換図式 が存在するときに、(A の B による拡大として)同値 であるという。
5項補題 により、真ん中の縦の矢印は同型である。A の B による拡大が、自明な拡大
0
→
B
→
A
⊕
B
→
A
→
0
{\displaystyle 0\rightarrow B\rightarrow A\oplus B\rightarrow A\rightarrow 0}
と同値であれば、分裂 (split)といわれる。
A の B による拡大
0
→
B
→
E
→
A
→
0
{\displaystyle 0\rightarrow B\rightarrow E\rightarrow A\rightarrow 0}
の同値類 と、
Ext
R
1
(
A
,
B
)
{\displaystyle \operatorname {Ext} _{R}^{1}(A,B)}
の元との間には、全単射な対応がある。
2つの拡大
0
→
B
→
E
→
A
→
0
{\displaystyle 0\rightarrow B\rightarrow E\rightarrow A\rightarrow 0}
0
→
B
→
E
′
→
A
→
0
{\displaystyle 0\rightarrow B\rightarrow E^{\prime }\rightarrow A\rightarrow 0}
が与えられると、ベール和 (Baer sum)と呼ばれる
A
{\displaystyle A}
引き戻し (pullback)
Γ
=
{
(
e
,
e
′
)
∈
E
⊕
E
′
|
g
(
e
)
=
g
′
(
e
′
)
}
.
{\displaystyle \Gamma =\left\{(e,e')\in E\oplus E'\;|\;g(e)=g'(e')\right\}.}
が得られる。
関係式
(
f
(
b
)
+
e
,
e
′
)
∼
(
e
,
f
′
(
b
)
+
e
′
)
{\displaystyle (f(b)+e,e')\sim (e,f'(b)+e')}
Y
=
Γ
/
{
(
f
(
b
)
,
0
)
−
(
0
,
f
′
(
b
)
)
|
b
∈
B
}
{\displaystyle Y=\Gamma /\{(f(b),0)-(0,f'(b))\;|\;b\in B\}}
をとると、拡大
0
→
B
→
Y
→
A
→
0
{\displaystyle 0\rightarrow B\rightarrow Y\rightarrow A\rightarrow 0}
が得られる。ここに第一の → は
b
↦
[
(
f
(
b
)
,
0
)
]
=
[
(
0
,
f
′
(
b
)
)
]
{\displaystyle b\mapsto [(f(b),0)]=[(0,f'(b))]}
(
e
,
e
′
)
↦
g
(
e
)
=
g
′
(
e
′
)
{\displaystyle (e,e')\mapsto g(e)=g'(e')}
拡大による同値類を同一視すると、ベール和は可換であり、自明な拡大を恒等元として持っている。拡大 0 → B → E → A → 0 は、射 g を -g に置き換えること反対の eg であり、真ん中の矢の逆にした拡大と同じである。
拡大の同値類を同一視した集合はアーベル群 であり、関手
E
x
t
R
1
(
A
,
B
)
{\displaystyle Ext_{R}^{1}(A,B)}
ベール和の見方は、Ext1Ab (A, B) の定義を、射影加群 や入射加群 といった観点なしでも、アーベル圏 (圏が射影加群や入射加群をもたない加群であっても)上で Ext関手を定義することが可能となる。単純に、Ext1Ab (A, B) を B による A の拡大の同値類の集合とすると、ベール和の下のアーベル群が形成される。同様に、高次 Ext群 ExtnAb (A, B) も n-拡大の同値類 として定義することができる。ここで n-拡大とは完全列
0
→
B
→
X
n
→
⋯
→
X
1
→
A
→
0
{\displaystyle 0\rightarrow B\rightarrow X_{n}\rightarrow \cdots \rightarrow X_{1}\rightarrow A\rightarrow 0}
であり、同値関係 は、すべての m ∈ {1, 2, ..., n} に対し写像 Xm → X'm が存在して可換図式 となるような、つまり鎖写像 (chain map)
X
:
ξ
→
ξ
{\displaystyle X:\xi \rightarrow \xi }
ξ
:
0
→
B
→
X
n
→
⋯
→
X
1
→
A
→
0
{\displaystyle \xi :0\rightarrow B\rightarrow X_{n}\rightarrow \cdots \rightarrow X_{1}\rightarrow A\rightarrow 0}
ξ
′
:
0
→
B
→
X
n
′
→
⋯
→
X
1
′
→
A
→
0
{\displaystyle \xi ':0\rightarrow B\rightarrow X'_{n}\rightarrow \cdots \rightarrow X'_{1}\rightarrow A\rightarrow 0}
の同一視から生成される。
上記の 2つの n-拡大のベール和は、X′′ を A 上のX1 と X′ の引き戻し (pullback)、'X′′ をXn と X′ の B の下の押し出し (英語版 )
0
→
B
→
X
n
″
→
X
n
−
1
⊕
X
n
−
1
′
→
⋯
→
X
2
⊕
X
2
′
→
X
1
″
→
A
→
0
{\displaystyle 0\rightarrow B\rightarrow X''_{n}\rightarrow X_{n-1}\oplus X'_{n-1}\rightarrow \cdots \rightarrow X_{2}\oplus X'_{2}\rightarrow X''_{1}\rightarrow A\rightarrow 0}
として定義される。
Ext関手は、計算に有益な便利な性質をいくつか持っている。
B が入射加群 であるか、または、A が射影加群 であれば、i > 0 に対して、Exti (A, B) = 0 である。 逆も成立する。すべての A に対して Ext1 (A, B) = 0 であれば、すべての A に対し Exti (A, B) = 0 で、かつ B は入射的である。すべての B に対し Ext1 (A, B) = 0 であれば、すべての B に対し Exti (A, B) = 0 でかつ A は射影的である。
Ext
R
n
(
⨁
α
A
α
,
B
)
≅
∏
α
Ext
R
n
(
A
α
,
B
)
{\displaystyle \operatorname {Ext} _{R}^{n}\left(\bigoplus _{\alpha }A_{\alpha },B\right)\cong \prod _{\alpha }\operatorname {Ext} _{R}^{n}(A_{\alpha },B)}
Ext
R
n
(
A
,
∏
β
B
β
)
≅
∏
β
Ext
R
n
(
A
,
B
β
)
{\displaystyle \operatorname {Ext} _{R}^{n}\left(A,\prod _{\beta }B_{\beta }\right)\cong \prod _{\beta }\operatorname {Ext} _{R}^{n}(A,B_{\beta })}
Ext関手を理解するもう一つの非常に有用な方法は以下の通りである: Extn (A, B) = 0 の要素を、A の射影分解 P* に対し、写像 f: Pn → B の同値類と考えると、B で終わる長完全系列 Q* を得て、次数 -n の鎖写像 f* : P* → Q* へ、加群 Pm の射影性を使い写像 f を持ち上げる(lift)ことができる。そのような鎖写像のホモトピー類 は、正確に上記の Ext関手の定義の同値類に対応することが分かる。
たとえば環 R が体 k や、k-代数 (algebra)の上の群環 のような、十分に良い条件下では、Ext* (k, k) に環の構造を入れることができる。積は同値な非常に多くの解釈を持ち、この解釈は Ext* (k, k) の元の様々な解釈に対応している。
ひとつの解釈として、鎖写像のこれらのホモトピー類の項として解釈がある。従って、2つの元の積は、対応する表現の成分により表現される。すると、k の分解をひとつ選ぶだけで、すべての計算が HomR (P* ,P* ) の中でできるようになり、これがまさに ExtR (k,k) をコホモロジーとしてもつ微分次数付き環である。
Ext群もまた、完全系列のことばで解釈することができる。このことは、射影加群や入射加群の存在に依存しないという優位性を持っている。従って、上記の観点では、Extn (A, B) は、ある同値関係の下で、B で始まり、A で終わる長さ n + 2 の完全系列のクラスとなる。従って、これは ... → X1 → A → 0 と 0 → A → Yn → ... を
⋯
→
X
1
→
Y
n
→
⋯
{\displaystyle \cdots \rightarrow X_{1}\rightarrow Y_{n}\rightarrow \cdots }
で置き換えることにより、Extm (C, A) の元とつなぎ合わされる。ここの中の矢印は、函数 X1 → A と A → Yn の合成である。積は米田接合積 と呼ばれる。
これらの観点は、双方で意味を持つ場合は常に同値となる。
同様の解釈の下で、充分に良い条件下では、再び、Ext* (k, M) は Ext* (k, k) 上の加群 である。
Z
[
G
]
{\displaystyle \mathbb {Z} [G]}
群 G の群環 とすると、
Ext
Z
[
G
]
∗
(
Z
,
M
)
{\displaystyle {\text{Ext}}_{\mathbb {Z} [G]}^{*}(\mathbb {Z} ,M)}
群コホモロジー
H
∗
(
G
,
M
)
{\displaystyle H^{*}(G,M)}
p 個の元を持つ有限体 F p に対し、
H
∗
(
G
,
M
)
=
Ext
F
p
[
G
]
∗
(
F
p
,
M
)
{\displaystyle H^{*}(G,M)={\text{Ext}}_{\mathbb {F} _{p}[G]}^{*}(\mathbb {F} _{p},M)}
A が k-代数 とすると、
Ext
A
⊗
k
A
o
p
∗
(
A
,
M
)
{\displaystyle {\text{Ext}}_{A\otimes _{k}A^{op}}^{*}(A,M)}
ホッホシルトコホモロジー (英語版 )
H
H
∗
(
A
,
M
)
{\displaystyle HH^{*}(A,M)}
R が可換環 k 上のリー代数
g
{\displaystyle {\mathfrak {g}}}
普遍包絡代数 であれば、
Ext
R
∗
(
k
,
M
)
{\displaystyle {\text{Ext}}_{R}^{*}(k,M)}
リー代数コホモロジー (英語版 )
H
∗
(
g
,
M
)
{\displaystyle \operatorname {H} ^{*}({\mathfrak {g}},M)}
^ injectiveは、「単射的」「移入的」とも呼ばれる。
Gelfand, Sergei I.; Manin, Yuri Ivanovich (1999), Homological algebra , Berlin: Springer, ISBN 978-3-540-65378-3 Weibel, Charles A. (1994), An introduction to homological algebra , Cambridge Studies in Advanced Mathematics, 38 , Cambridge University Press , ISBN 978-0-521-55987-4 , OCLC 36131259 , MR 1269324 








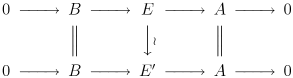







![{\displaystyle b\mapsto [(f(b),0)]=[(0,f'(b))]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee75b87481bf9de19754e30ff4b98f9e3a93c53f)










![{\displaystyle \mathbb {Z} [G]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f40260c366fc309a5872899d2ea34cf094855857)
![{\displaystyle {\text{Ext}}_{\mathbb {Z} [G]}^{*}(\mathbb {Z} ,M)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c3404818eb528ea2a4d4025ec528d60495129a9)

![{\displaystyle H^{*}(G,M)={\text{Ext}}_{\mathbb {F} _{p}[G]}^{*}(\mathbb {F} _{p},M)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/087c0c38661aefc2bfd7eafed1141fe24cf644b3)




