疫学における区画モデル

区画モデル（くかくモデル、英: Compartmental model）は、単純かつ一般的な感染症の数理モデル化の方法の総称である。区画モデルでは、集団内の個体は、感染状態に応じて、それぞれ「区画」と呼ばれるラベルを割り当てられる。例えば、S、I、Rという区画は、それぞれSusceptible〈感受性保持者〉、Infectious〈感染者〉、Recovered〈免疫保持者〉を表す。個体は感染状態の進行にともなって、区画間を移行する。具体的な区画モデルは、例えばSIRモデル、SIESモデルなどと呼ばれるが、こうしたモデルの名称となるラベルの順番は通常、区画間の移行のパターンを示している。例えば、SEISは、感受性（susceptible）、曝露（exposed）、感染（infectious）、そして再び感受性（susceptible）の順に感染状態が進行することを意味する。

こういったモデルの起源は20世紀初頭であり、1927年のカーマックとマッケンドリックの研究が重要である。

モデルは（決定論的である）常微分方程式を用いて実行されることが多いが、確率論的（ランダム）な枠組みを用いることも可能である。確率論的モデルはより現実的ではあるが解析がはるかに複雑である。

モデルは、病気がどのように広がるか、感染者の総数、流行の期間などを予測し、再生産数などの様々な疫学的パラメータを推定しようとする。このようなモデルは、異なる公衆衛生上の介入が流行の結果にどのように影響を与えるかを示すことができる。例えば、与えられた集団に限られた数のワクチンを接種するために最も効率的な手法は何かを示すことができる。

SIRモデル

→詳細は「SIRモデル」を参照

SIRモデルは最も単純な区画モデルの1つであり、多くのモデルはこの基本形から派生している。本モデルは3つの区画で構成されている。

S

感受性（susceptible）個体の数。感受性個体と感染個体が「感染性接触」すると、感受性個体が病気に感染し、感染性区画に移行する。

I

感染（infectious）個体数のこと。感染した個体であり、感受性個体を感染させる可能性がある。

R

隔離（removed）（免疫のある）個体、または死亡した個体の数。これらは、感染から回復して隔離区画に入った個体、または死亡した個体である。死亡者数は総人口に対して無視できるほどの数であると仮定している。この区画を「回復（recovered）」または「抵抗性（resistant）」と呼ぶこともある。

このモデルは、麻疹、おたふくかぜ、風疹といった、回復が持続的な抵抗性をもたらし、ヒトからヒトへ感染する感染症について合理的に予測可能である。

空間SIRモデルシミュレーション。個々のセルは隣接した8つの区画を感染させることができる。

これらの変数（S、I、R）は、特定の時間に各区画にいる人の数を表す。感受性個体、感染個体、隔離個体の数が（総人口サイズが一定であっても）時間とともに変化する可能性があることを表すために、正確な数をt（時間）の関数S(t)、I(t)、R(t) とする。特定の集団における特定の疾患については、これらの関数は、可能性のあるアウトブレイクを予測し、それらを制御下に置くために働くかもしれない。

SIRモデルは3つの意味で動的である

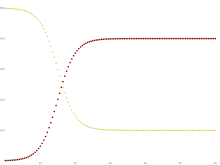
tの変数関数で表わされるように、本モデルは各区画内の数が時間の経過とともに変動するという意味で動的である。この動的な側面の重要性は、1968年にワクチンが導入される前の英国の麻疹のように、感染期間が短い風土病において最も明白である。このような病気は、感受性保持者数（S(t)）が時間の経過とともに変化するため、何度も流行する傾向がある。伝染病が流行すると、より多くの感受性保持者が感染区画に入るため、感受性保持者の数が急激に減少し、彼らは感染区画と隔離区画に入ることになる。生まれた子どもが感受性区画に入るなどして、感受性個体の数が回復するまでは、病気が再び流行することはできない。

黄色=感受性、えび茶色=感染、鴨の羽色=回復

集団の各メンバーは、通常、感受性区画から感染性区画へ、そして隔離区画へと進行する。これは以下のような、箱が異なる区画を表し、矢印が区画間の遷移を表すフロー図として示すことができる。

SIR compartment model

遷移速度

モデルを完全に明確に記述するためには、矢印を区画間の遷移速度でラベル付けするべきである。SとIの間では、遷移速度をd(S/N)/dt = -βSI/N²と仮定する。ここで、Nは総人口、βは時間当たりの1人当たりの平均接触数に感受性保持者と感染者の間の接触における病気の伝播確率を乗じたもの、SI/N²は感受性保持者と感染者の間の接触のうち、感受性保持者が感染することになる接触の割合である（これは数学的には、分子間のランダムな衝突が化学反応を引き起こし、分率が2つの反応物の濃度に比例するという化学の質量作用の法則に似ている）。

IとRの間では、遷移速度は感染個体数に比例すると仮定し、これをγIとする。これは、任意の時間間隔dtにおいて感染個体が回復する確率が単純にγdtであると仮定していることと等価である。ある個体が平均的な時間間隔Dで感染している場合、γ = 1/Dとなる。これは、個人が感染状態にある時間の長さが指数分布を持つランダム変数であるという仮定と等価である。この「古典的」SIRモデルは、I-R遷移速度のためにより複雑で現実的な分布（例えば、アーラン分布）を使用することによって修正することができる。

感染区画からの除去（隔離）がない特別な場合 (γ=0) では、SIRモデルは、すべての個体が最終的に感染するロジスティック解を持つ非常に単純なSIモデルに簡約される。

SIRモデルの生物数理学的・決定論的取り扱い

人口動態がないSIRモデル

伝染病（例えばインフルエンザ）の動態は、出生と死亡の動態よりもはるかに速いことが多いため、単純な区画モデルでは出生と死亡が省略されることが多い。先に述べたいわゆる人口動態（出生および死亡）を考慮しないSIRシステムは以下の一組の常微分方程式で表わすことができる。

${\begin{aligned}&{\frac {dS}{dt}}=-{\frac {\beta IS}{N}},\\[6pt]&{\frac {dI}{dt}}={\frac {\beta IS}{N}}-\gamma I,\\[6pt]&{\frac {dR}{dt}}=\gamma I.\end{aligned}}$

上式において、$S$は感受性集団のストック、$I$は感染集団のストック、$R$は隔離集団のストック（死亡または回復による）、そして$N$ はこれら3つの和である。

このモデルは、ウィリアム・オグルヴィ・カーマックとアンダーソン・グレイ・マッケンドリックによって、現在カーマック・マッケンドリック理論と呼ばれているものの特別な場合として初めて提案されたものであり、マッケンドリックがロナルド・ロスと共に行った研究に続いて行われた。

このシステムは非線形であるが、陰関数形式でその解析解を導出することが可能である。他の数値計算ツールとしては、ギレスピー・アルゴリズムといったモンテカルロ法がある。

第1に、

${\frac {dS}{dt}}+{\frac {dI}{dt}}+{\frac {dR}{dt}}=0$

から、

$S(t)+I(t)+R(t)={\text{一定}}=N$

となる。この式は数学的に人口$N$の恒常性を表わしている。

ここで留意すべきは、上記の関係は3つの変数のうち2つに関する式だけを調べる必要があることを示唆している点である。

第2に、伝染病クラスの動態が比率

$R_{0}={\frac {\beta }{\gamma }},$

いわゆる基本再生産数（基本再生産率とも）に依存することに注目する。この比率は、すべての対象者が感受性である集団における1つの感染からの新規感染（これらの新規感染は二次感染と呼ばれることもある）の予想数として導き出される。この考えは、接触の間の典型的な時間は $T_{c}=\beta ^{-1}$であり、隔離までの典型的な時間は $T_{r}=\gamma ^{-1}$であると言えば、おそらくもっとわかりやすいだろう。ここから、平均して、感染者が隔離される「前」に他の人と接触した回数は$T_{r}/T_{c}$となる。

1つ目の微分方程式を3つ目の微分方程式で割って、変数を分離して積分すると以下のようになる。

$S(t)=S(0)e^{-R_{0}(R(t)-R(0))/N}$

上式において、$S(0)$および$R(0)$はそれぞれ感受性保持者および隔離者の初期数である。感受性保持者の初期割合を$s_{0}=S(0)/N$、極限$t\to \infty$における感受性保持者および隔離者の割合をそれぞれ$s_{\infty }=S(\infty )/N$および$r_{\infty }=R(\infty )/N$と書くと。

$s_{\infty }=1-r_{\infty }=s_{0}e^{-R_{0}(r_{\infty }-r_{0})}$

となる（ここで留意すべきは、感染区画はこの極限において空になる点である）。この超越方程式はランベルトW関数の観点において解を持つ、すなわち

$s_{\infty }=1-r_{\infty }=-R_{0}^{-1}\,W(-s_{0}R_{0}e^{-R_{0}(1-r_{0})})$

となる。これは、エピデミックの終わりには、$s_{0}=0$でない限り、集団のすべての個体が隔離されたわけではないので、一部は感受性のままであることを示している。これは、エピデミックの終わりは、感受性保持者の絶対的な不足ではなく、感染者の数が減少することによって引き起こされることを意味する。

基本再生産数の役割は極めて重要である。実際、感染者に関する方程式を

${\frac {dI}{dt}}=\left(R_{0}{\frac {S}{N}}-1\right)\gamma I$

と書き換えると、もし

$R_{0}>{\frac {N}{S(0)}}$

ならば、

${\frac {dI}{dt}}(0)>0$

となる。すなわち、（人口のかなりの割合に達することができる）感染者数の増加を伴う相応のエピデミックなアウトブレイクがあるだろう。逆に、もし

$R_{0}<{\frac {N}{S(0)}}$

ならば、

${\frac {dI}{dt}}(0)<0$

となる。すなわち、感受性保持者集団の初期の規模とは無関係に、この病気が相応のエピデミックなアウトブレイクを引き起こすことはあり得ない。結果として、基本再生産数が極めて重要であることは明らかである。

感染力

ここで留意すべきは、上述したモデルにおいて、関数

$F=\beta I$

は、感受性保持者の区画から感染者の区画への遷移速度をモデル化し、これを感染力と呼ぶ。しかしながら、伝染病の多くのグループについては、感染力は感染者の絶対数に依存せず、（一定総人口に対する$N$に対する）感染者の割合に依存すると考える方がより現実的である。

$F=\beta {\frac {I}{N}}$

Capassoと、その後、他の著者らは、伝染過程をより現実的にモデル化するために、非線形感染力を提案した。

SIRモデルの厳密な解析解

2014年は、Harkoと共著者らは、SIRモデルの厳密な解析解を導出した。人口動態が設定されていない場合、${\mathcal {S}}(u)=S(t)$などは、

$t={\frac {N}{\beta }}\int _{u}^{1}{\frac {du^{*}}{u^{*}{\mathcal {I}}(u^{*})}},\quad \rho ={\frac {\gamma N}{\beta }},$

に関して、次のような時間パラメータ化に対応する。

${\mathcal {S}}(u)=S(0)u$

${\mathcal {I}}(u)=N-{\mathcal {R}}(u)-{\mathcal {S}}(u)$

${\mathcal {R}}(u)=R(0)-\rho \ln(u)$

初期条件は

$t={\frac {N}{\beta }}\int _{u}^{1}{\frac {du^{*}}{u^{*}{\mathcal {I}}(u^{*})}},\quad \rho ={\frac {\gamma N}{\beta }}$

であり、$u_{T}$は${\mathcal {I}}(u_{T})=0$を満たす。

上述した$R_{\infty }$に関する超越方程式によって、$u_{T}=e^{-(R_{\infty }-R(0))/\rho }(=S_{\infty }/S(0)$ if $S(0)\neq 0)$および$I_{\infty }=0$となる。

Millerによって見出された等価な解析解により

${\begin{aligned}S(t)&=S(0)e^{-\xi (t)}\\[8pt]I(t)&=N-S(t)-R(t)\\[8pt]R(t)&=R(0)+\rho \xi (t)\\[8pt]\xi (t)&={\frac {\beta }{N}}\int _{0}^{t}I(t^{*})\,dt^{*}\end{aligned}}$

が得られる。

ここで、$\xi (t)$は、個人が時刻$t$までに受け取った伝染の期待値と解釈することができる。これらの2つの解は$e^{-\xi (t)}=u$でつながっている。

事実上、同じ結果はカーマックとマッケンドリックの最初の論文にも見出すことができる。

これらの解は、元の微分方程式の右辺のすべての項が$I$に比例していることに注意すれば、簡単に理解できるかもしれない。したがって、方程式を$I$で割って、左辺の微分演算子が単純に$d/d\tau$（$d\tau =Idt$、すなわち$\tau =\int Idt$）になるように、時間を再スケーリングすることができる。これで微分方程式はすべて線形となり、$dR/d\tau =$ 定数の形式の第3の方程式は、$\tau$と$R$（および上記の$\xi$）が単純に線形に関係していることを示している。

人口動態があり人口一定のSIRモデル

死亡率$\mu$および出生率$\Lambda$によって特徴付けられ、伝染病が蔓延している母集団を考えてみる。質量作用伝播を持つモデルは

${\begin{aligned}{\frac {dS}{dt}}&=\Lambda -\mu S-{\frac {\beta IS}{N}}\\[8pt]{\frac {dI}{dt}}&={\frac {\beta IS}{N}}-\gamma I-\mu I\\[8pt]{\frac {dR}{dt}}&=\gamma I-\mu R\end{aligned}}$

であり、このモデルに対する感染症の無い平衡解（disease-free equilibrium: DFE）は

$\left(S(t),I(t),R(t)\right)=\left({\frac {\Lambda }{\mu }},0,0\right)$

である。

この場合、基本再生産数

$R_{0}={\frac {\beta \Lambda }{\mu (\mu +\gamma )}}$

を導出することができ、これは閾値特性を有さない。実際、生物学的に意味を持つ初期値から独立に、以下を示すことができる。

$R_{0}\leq 1\Rightarrow \lim _{t\to \infty }(S(t),I(t),R(t))={\textrm {DFE}}=\left({\frac {\Lambda }{\mu }},0,0\right)$

$R_{0}>1,I(0)>0\Rightarrow \lim _{t\to \infty }(S(t),I(t),R(t))={\textrm {EE}}=\left({\frac {\gamma +\mu }{\beta }},{\frac {\mu }{\beta }}\left(R_{0}-1\right),{\frac {\gamma }{\beta }}\left(R_{0}-1\right)\right)$

点EEはエンデミックな平衡解（Endemic Equilibrium）と呼ばれる（疫病は根絶されず、母集団に留まる）。ヒューリスティックな論証によって、$R_{0}$は完全に感受性な集団の中で1人の感染者によって引き起こされた平均感染数として読めることを示すことができる。上記の関係は、生物学的には、この数が1以下であれば病気は絶滅し、1以上であれば病気は永久に集団の中で流行し続けることを意味する。

SISモデル

黄色=感受性, えび茶色=感染

風邪やインフルエンザなどの感染症の中には、長期的な免疫が得られないものがある。このような感染症は、感染から回復しても免疫力が得られず、再び感受性となる。

SIS区画モデル

モデルは

${\begin{aligned}{\frac {dS}{dt}}&=-{\frac {\beta SI}{N}}+\gamma I\\[6pt]{\frac {dI}{dt}}&={\frac {\beta SI}{N}}-\gamma I\end{aligned}}$

である。

ここで留意すべきは、総人口をNで表わすと、

${\frac {dS}{dt}}+{\frac {dI}{dt}}=0\Rightarrow S(t)+I(t)=N$

が成り立つことである。すると、

${\frac {dI}{dt}}=(\beta -\gamma )I-{\frac {\beta }{N}}I^{2}$

となる。すなわち、感染の動態はロジスティック関数で支配されている。$\forall I(0)>0$:

${\begin{aligned}&{\frac {\beta }{\gamma }}\leq 1\Rightarrow \lim _{t\to +\infty }I(t)=0,\\[6pt]&{\frac {\beta }{\gamma }}>1\Rightarrow \lim _{t\to +\infty }I(t)=\left(1-{\frac {\gamma }{\beta }}\right)N\end{aligned}}$

基本再生産数が1よりも大きいような、（変数の変換$I=y^{-1}$を行い、これを平均場方程式に代入することによって）このモデルの解析的解を見つけることができる。解は以下の通りである。

$I(t)={\frac {I_{\infty }}{1+Ve^{-\chi t}}}$

上式において、$I_{\infty }=(1-\gamma /\beta )N$は伝染感染集団、$\chi =\beta -\gamma$、$V=I_{\infty }/I_{0}-1$である。この系は閉じていると仮定されるため、感受性保持者集団は$S(t)=N-I(t)$となる。

特殊な場合として、$\gamma =0$と仮定することによって普通のロジスティック関数が得られる。これは、$R=0$、すなわち隔離が起こらないSIRモデルにおいても考慮することができる。これは「SIモデル」である。$S=N-I$を用いる微分方程式はしたがって、

${\frac {dI}{dt}}\propto I\cdot (N-I).$

と簡約される。

長期的には、このモデルでは、すべての個体が感染することになる。

基本的なSIRモデルの精緻化

SIRDモデル

SIRDモデルの模式図。初期値$S(0)=997,I(0)=3,R(0)=0$、感染率$\beta =0.4$、回復率$\gamma =0.035$、死亡率$\mu =0.005$。

SIRDモデルのアニメーション。初期値${\textstyle S(0)=997,I(0)=3,R(0)=0}$、感染率初期値${\textstyle \beta =0.5}$、回復率（一定）${\textstyle \gamma =0.035}$、死亡率（一定）${\textstyle \mu =0.005}$。利用可能な薬も予防接種もない場合は、適切な対策（例えば「社会距離拡大戦略（ソーシャル・ディスタンシング）」など）によって感染率を下げる（「カーブを平らにする」としばしば言われる）ことしかできない。このアニメーションは、感染率を76%減少させた場合（${\textstyle \beta =0.5}$から${\textstyle \beta =0.12}$に低減）の効果を示している。

「感受性-感染-回復-死亡モデル」（Susceptible-Infectious-Recovered-Deceased-Model）は、「回復」（具体的には、病気を生き延びて免疫を得た個体を意味する）と「死亡」を区別する。このモデルでは、以下の微分方程式の系を使用する。

${\begin{aligned}&{\frac {dS}{dt}}=-{\frac {\beta IS}{N}},\\[6pt]&{\frac {dI}{dt}}={\frac {\beta IS}{N}}-\gamma I-\mu I,\\[6pt]&{\frac {dR}{dt}}=\gamma I,\\[6pt]&{\frac {dD}{dt}}=\mu I,\end{aligned}}$

上式において、$\beta ,\gamma ,\mu$はそれぞれ感染率、回復率、死亡率である。

MSIRモデル

麻疹を含む多くの感染症では、新生児は感受性区間へは入らず、生後数か月間は母体由来の抗体（胎盤を介して、さらに初乳を介して伝達される）による保護のために、病気に対する免疫を持っている。これは受動免疫と呼ばれる。この追加の詳細は、モデルの最初にMクラス（母体由来の免疫）を含めることによって示すことができる。

MSIR compartmental model

これを数学的に示すために、追加の区間M(t) が追加される。これにより、次のような微分方程式が得られる。

${\begin{aligned}{\frac {dM}{dT}}&=\Lambda -\delta M-\mu M\\[8pt]{\frac {dS}{dT}}&=\delta M-{\frac {\beta SI}{N}}-\mu S\\[8pt]{\frac {dI}{dT}}&={\frac {\beta SI}{N}}-\gamma I-\mu I\\[8pt]{\frac {dR}{dT}}&=\gamma I-\mu R\end{aligned}}$

キャリア状態

結核といった感染症にかかったことのある人の中には、完全に回復することはなく、病気自体には罹患していないものの、感染症を抱え続けている人もいる。彼らはその後、再び感染区画に移動し、（結核のように）症状に苦しむかもしれない。または彼らは症状に苦しんでいない間、キャリア状態で他の人に感染し続けるかもしれない。最も有名な例は、22人を腸チフスに感染させたメアリー・マロンであろう。キャリア区画はCとラベル付けされる。

SEIRモデル

→詳細は「SEIRモデル」を参照

多くの重要な感染症では、個体は感染しているが、まだ発症していない潜伏期間が存在する。この期間中、個体は区画E（exposed）にいる。

SEIR compartmental model

潜伏期間がパラメータ$a$を持つ指数分布の確率変数であると仮定し（すなわち、平均潜伏期間は$a^{-1}$）、また、出生率$\Lambda$が死亡率$\mu$に等しい人口動態の存在を仮定すると、モデルは次のようになる。

${\begin{aligned}{\frac {dS}{dt}}&=\mu N-\mu S-\beta {\frac {I}{N}}S\\[8pt]{\frac {dE}{dt}}&=\beta {\frac {I}{N}}S-(\mu +a)E\\[8pt]{\frac {dI}{dt}}&=aE-(\gamma +\mu )I\\[8pt]{\frac {dR}{dt}}&=\gamma I-\mu R.\end{aligned}}$

ここで、$S+E+I+R=N$であるが、 これは、出生率と死亡率が等しいという（縮退した）仮定のために一定であるだけで、一般的に$N$は変数である。

このモデルについて、基本再生産数は

$R_{0}={\frac {a}{\mu +a}}{\frac {\beta }{\mu +\gamma }}$

である。

SIRモデルと同様に、この場合においても、感染症の無い平衡解（DFE: N,0,0,0）とエンデミックな平衡解（EE）があり、生物学的に意味を持つ初期条件とは独立に以下を示すことができる。

$\left(S(0),E(0),I(0),R(0)\right)\in \left\{(S,E,I,R)\in [0,N]^{4}:S\geq 0,E\geq 0,I\geq 0,R\geq 0,S+E+I+R=N\right\}$

これは

$R_{0}\leq 1\Rightarrow \lim _{t\to +\infty }\left(S(t),E(t),I(t),R(t)\right)=DFE=(N,0,0,0),$

$R_{0}>1,I(0)>0\Rightarrow \lim _{t\to +\infty }\left(S(t),E(t),I(t),R(t)\right)=EE$

を満たす。

接触率$\beta (t)$が周期的に変化する場合、DFEの大域的誘引性の条件は、周期的な係数を持つ以下の線形系

${\begin{aligned}{\frac {dE_{1}}{dt}}&=\beta (t)I_{1}-(\gamma +a)E_{1}\\[8pt]{\frac {dI_{1}}{dt}}&=aE_{1}-(\gamma +\mu )I_{1}\end{aligned}}$

が安定なことである（すなわち、複素平面における単位円内にフロケの固有値を持つ）。

SEISモデル

SEISモデルは、最後に免疫が獲得できないことを除けば、SEIRモデル（上）と同様である。

${\color {blue}{{\mathcal {S}}\to {\mathcal {E}}\to {\mathcal {I}}\to {\mathcal {S}}}}$

このモデルでは、感染は免疫を残さないので、回復した個体は再び感受性のある状態に戻り、S(t') 区画に後退する。以下の微分方程式はこのモデルを記述している。

${\begin{aligned}{\frac {dS}{dT}}&=\Lambda -{\frac {\beta SI}{N}}-\mu S+\gamma I\\[6pt]{\frac {dE}{dT}}&={\frac {\beta SI}{N}}-(\epsilon +\mu )E\\[6pt]{\frac {dI}{dT}}&=\varepsilon E-(\gamma +\mu )I\end{aligned}}$

MSEIRモデル

受動免疫の要因と潜伏期間を持つ疾患の場合には、MSEIRモデルが存在する。

$\color {blue}{{\mathcal {M}}\to {\mathcal {S}}\to {\mathcal {E}}\to {\mathcal {I}}\to {\mathcal {R}}}$

${\begin{aligned}{\frac {dM}{dT}}&=\Lambda -\delta M-\mu M\\[6pt]{\frac {dS}{dT}}&=\delta M-{\frac {\beta SI}{N}}-\mu S\\[6pt]{\frac {dE}{dT}}&={\frac {\beta SI}{N}}-(\varepsilon +\mu )E\\[6pt]{\frac {dI}{dT}}&=\varepsilon E-(\gamma +\mu )I\\[6pt]{\frac {dR}{dT}}&=\gamma I-\mu R\end{aligned}}$

MSEIRSモデル

MSEIRSモデルはMSEIRに似ているが、Rクラスの免疫は一時的なものであり、一時的な免疫が終了すると個人は再び感受性を取り戻すことになる。

${\color {blue}{{\mathcal {M}}\to {\mathcal {S}}\to {\mathcal {E}}\to {\mathcal {I}}\to {\mathcal {R}}\to {\mathcal {S}}}}$

変動する接触率、年複数回またはカオス的流行

病気にかかる確率は時間的に一定ではないことはよく知られている。風邪ウイルスといった季節性のある病気もあり、これらは冬季に流行しやすくなる。麻疹、おたふくかぜ、風疹などの小児の病気では、学校暦との相関関係が強く、学校が休みの間はかかる確率が激減する。

結果として、多くの疾患では、周期的に（季節的に）変化する接触率

$F=\beta (t){\frac {I}{N}},\quad \beta (t+T)=\beta (t)$

を持つ感染力を考慮する必要がある（周期Tは1年に等しい）。

したがって、モデルは

${\begin{aligned}{\frac {dS}{dt}}&=\mu N-\mu S-\beta (t){\frac {I}{N}}S\\[8pt]{\frac {dI}{dt}}&=\beta (t){\frac {I}{N}}S-(\gamma +\mu )I\end{aligned}}$

となる（回復の動態は簡単に$R=N-S-I$となる）。すなわち、周期的に変化するパラメータを持つ微分方程式の非線形集合である。このクラスの力学系は非線形パラメトリック共鳴という非常に興味深く複雑な現象を経ることが知られている。

もし

${\frac {1}{T}}\int _{0}^{T}{\frac {\beta (t)}{\mu +\gamma }}\,dt<1\Rightarrow \lim _{t\to +\infty }(S(t),I(t))=DFE=(N,0),$

ならば容易に理解できるが、この積分が1よりも大きい場合、病気は消えず、こういった共鳴が存在するかもしれない。例えば、周期的に変化する接触率をシステムの「入力」として考えると、出力は周期が入力の周期の倍数である周期関数であることがわかる。これにより、いくつかの感染症の多年に1回の（通常は2年に1回の）流行の発生を、接触率の振動の周期と、エンデミックな平衡解近傍の減衰振動の疑似周期との間の相互作用として説明することができるようになった。驚くべきことに、いくつかの場合では、その挙動は準周期的なものであったり、カオス的なものであったりすることもある。

予防接種のモデル化

SIRモデルは、予防接種をモデル化するために修正することができる。典型的には、これらはSIRモデルに予防接種を受けた個人のための追加の区画$V$を導入する。以下、いくつかの例を示す。

新生児への予防接種

伝染病が発生している状況において、主要な課題の1つは、予防策を講じ、可能であれば、集団予防接種体制の確立によって、伝染病を根絶することである。新生児に接種率$P\in (0,1)$で（生涯免疫を与えるワクチンを）予防接種した場合を考えてみる。

${\begin{aligned}{\frac {dS}{dt}}&=\nu N(1-P)-\mu S-\beta {\frac {I}{N}}S\\[8pt]{\frac {dI}{dt}}&=\beta {\frac {I}{N}}S-(\mu +\gamma )I\\[8pt]{\frac {dV}{dt}}&=\nu NP-\mu V\end{aligned}}$

上式において、$V$は予防接種を受けた個人のクラスである。

$\lim _{t\to +\infty }V(t)=NP$

であることはすぐに分かる、したがって$S$と$I$,の長期的な振る舞いを扱うことにする。これらは

$R_{0}(1-P)\leq 1\Rightarrow \lim _{t\to +\infty }\left(S(t),I(t)\right)=DFE=\left(N\left(1-P\right),0\right)$

$R_{0}(1-P)>1,\quad I(0)>0\Rightarrow \lim _{t\to +\infty }\left(S(t),I(t)\right)=EE=\left({\frac {N}{R_{0}(1-P)}},N\left(R_{0}(1-P)-1\right)\right)$

を満たす。

つまり

$P<P^{*}=1-{\frac {1}{R_{0}}}$

ならば、予防接種計画は病気の根絶には成功せず、それどころか、ワクチン接種をしなかった場合よりは低いレベルではあるが、流行し続けることになる。つまり、この数理モデルは、基本再生産数が18ほど高い病気を根絶するためには、少なくとも94.4%の新生児にワクチンを接種する必要があることを示唆している。

予防接種と情報

現代社会は、「合理的な」免除、すなわち、感染からの知覚されるリスクとワクチンから損害を受けることによるリスクを「合理的」に比較した結果として、子供に予防接種受けさせないという家族の決断に直面している。この行動が本当に合理的であるかどうか、すなわち、それが等しく病気の根絶をもたらすことができるかどうかを評価するため、単に予防接種率が感染者数の増加関数

$P=P(I),\quad P'(I)>0$

であると仮定することができる。

このような場合、根絶条件は

$P(0)\geq P^{*}$

となる。すなわち、ベースライン予防接種率は、免除の場合は満たされない、「強制接種」の閾値以上でなければならない。このように、「合理的」な免除は、ワクチン接種率が高いために発生率が低い現状のみに基づいており、接種率の低下による将来の感染症再燃を考慮していないため、近視眼的である可能性がある。

新生児以外への予防接種

新生児以外にも率ρで予防接種を行う場合、感受性保持者と予防接種済みの人についての方程式は

${\begin{aligned}{\frac {dS}{dt}}&=\mu N(1-P)-\mu S-\rho S-\beta {\frac {I}{N}}S\\[8pt]{\frac {dV}{dt}}&=\mu NP+\rho S-\mu V\end{aligned}}$

と修正されなければならず、ここから次のような根絶条件が得られる。

$P\geq 1-\left(1+{\frac {\rho }{\mu }}\right){\frac {1}{R_{0}}}$

パルス予防接種戦略

→詳細は「パルス予防接種戦略」を参照

パルス予防接種戦略では、特定の年齢集団（幼児や高齢者など）にワクチンを接種することを繰り返す。この方法を用いると、感受性個体の集団は直ちに除去され、集団全体から（麻疹といった）感染症を排除することが可能となる。T時間単位毎に、感受性保持者の一定の割合pが（病気の動態に対して）比較的短い時間内に接種を受ける。これにより、感受性保持者と予防接種済みの集団について、次のようなインパルス微分方程式が導かれる。

${\begin{aligned}{\frac {dS}{dt}}&=\mu N-\mu S-\beta {\frac {I}{N}}S,\quad S(nT^{+})=(1-p)S(nT^{-}),&&n=0,1,2,\ldots \\[8pt]{\frac {dV}{dt}}&=-\mu V,\quad V(nT^{+})=V(nT^{-})+pS(nT^{-}),&&n=0,1,2,\ldots \end{aligned}}$

I = 0と設定することで、感受性保持者の動態が

$S^{*}(t)=1-{\frac {p}{1-(1-p)E^{-\mu T}}}E^{-\mu MOD(t,T)}$

で与えられ、根絶条件が

$R_{0}\int _{0}^{T}S^{*}(t)\,dt<1$

であることが容易にわかる。

年齢の影響: 年齢構造化モデル

年齢は集団における疾病伝播率、特に接触率に深く影響する。この接触率は、感受性保持者と感染者の接触の有効性を要約する。

$S(t)=\int _{0}^{a_{M}}s(t,a)\,da$

$I(t)=\int _{0}^{a_{M}}i(t,a)\,da$

$R(t)=\int _{0}^{a_{M}}r(t,a)\,da$

（$a_{M}\leq +\infty$は最大許容年齢）のように伝染病クラス$s(t,a),i(t,a),r(t,a)$の年齢を考慮に入れる（感受性-感染性-隔離スキームに限定するため）。それらの動態は「単純な」偏微分方程式によって記述されず、以下の積分微分方程式で記述される。

$\partial _{t}s(t,a)+\partial _{a}s(t,a)=-\mu (a)s(a,t)-s(a,t)\int _{0}^{a_{M}}k(a,a_{1};t)i(a_{1},t)\,da_{1}$

$\partial _{t}i(t,a)+\partial _{a}i(t,a)=s(a,t)\int _{0}^{a_{M}}{k(a,a_{1};t)i(a_{1},t)da_{1}}-\mu (a)i(a,t)-\gamma (a)i(a,t)$

$\partial _{t}r(t,a)+\partial _{a}r(t,a)=-\mu (a)r(a,t)+\gamma (a)i(a,t)$

上式において、

$F(a,t,i(\cdot ,\cdot ))=\int _{0}^{a_{M}}k(a,a_{1};t)i(a_{1},t)\,da_{1}$

は感染力であり、これは、当然、年齢間の相互作用に依存する。

新生児の初期条件（すなわち、a=0の場合）によって複雑さが付加される。この初期条件は感染区分および隔離区分については

$i(t,0)=r(t,0)=0$

と明快であるが、感受性を持つ新生児の密度については非局所的である。

$s(t,0)=\int _{0}^{a_{M}}\left(\varphi _{s}(a)s(a,t)+\varphi _{i}(a)i(a,t)+\varphi _{r}(a)r(a,t)\right)\,da$

上式において、$\varphi _{j}(a),j=s,i,r$は大人の出生率である。

さらに、現在の総人口$n(t,a)=s(t,a)+i(t,a)+r(t,a)$の密度を定義すると、

$\partial _{t}n(t,a)+\partial _{a}n(t,a)=-\mu (a)n(a,t)$

が得られる。

3つの伝染病クラスにおいて出生率が等しい最も単純な場合において、人口均衡を保つためには、出生率$\varphi (.)$と死亡率$\mu (a)$を結び付ける以下の必要十分条件

$1=\int _{0}^{a_{M}}\varphi (a)\exp \left(-\int _{0}^{a}{\mu (q)dq}\right)\,da$

と人口均衡

$n^{*}(a)=C\exp \left(-\int _{0}^{a}\mu (q)\,dq\right),$

が満たされなけばならず、これによって自動的に感染症の無い解

$DFS(a)=(n^{*}(a),0,0).$

の存在が保証される。

基本再生産数は、適切な関数演算子のスペクトル半径として計算することができる。

区画感染症モデル内におけるその他の考慮事項

垂直感染

AIDSやB型肝炎といった一部の病気の場合、感染した両親の子どもが感染した状態で生まれることがある。このような母親からの伝染は垂直感染と呼ばれる。 感染区画への追加メンバーの流入は、感染区画に新生児の一部を含めることで、モデル内で考慮することができる。

媒介生物感染

ヒトからヒトへ間接的に伝染する病気（例えば、マラリアは蚊が媒介する）は媒介生物を介して伝播される。これらの場合、感染はヒトから昆虫へと移行し、伝染モデルは両方の種を含まなければならず、一般的には直接感染のモデルよりも多くの区画を必要とする。

その他

伝染病をモデル化する際に考慮する必要があるその他の事象としては、以下のようなものがある。

• 非一様混合
• 変動のある感染力
• 空間的に不均一な分布
• マクロパラサイトによって引き起こされる疾患

決定論的感染症モデル対確率的感染症モデル

ここで提示された決定論的モデルは、十分に大きな母集団の場合にのみ有効であることを強調することが重要であり、そのようなものとして慎重に使用されるべきである。

より正確には、これらのモデルは熱力学的極限においてのみ有効であり、ここでは母集団は実質的に無限大である。確率モデルでは、システム内で感染者の数が1人以下になる確率が有限であるため、上述した長期的なエンデミックな平衡解は成り立たない。真のシステムでは、感染する宿主がいないので、病原体は伝播しないかもしれない。しかし、決定論的平均場モデルでは、感染者数は実数、すなわち、感染した宿主の非整数値を取ることができ、モデル内の宿主の数は1以下であっても、0以上であってもよく、それによってモデル内の病原体が伝播することが可能となる。

推奨文献

• May, Robert M.; Anderson, Roy M. (1991). Infectious diseases of humans: dynamics and control. Oxford: Oxford University Press. ISBN 0-19-854040-X 
• Capasso, V. (1993). Mathematical Structure of Epidemic Systems. Berlin: Springer. ISBN 3-540-56526-4 
• Vynnycky, E.; White, R. G., eds (2010). An Introduction to Infectious Disease Modelling. Oxford: Oxford University Press. ISBN 978-0-19-856576-5 

関連項目

• 感染症の数理モデル化
• 可変単位地区問題
• 次世代行列
• リスクアセスメント
• 罹患率
• モデリング (科学的)

外部リンク

• SIR model: Online experiments with JSXGraph
• Simulating an epidemic - YouTube