ダイアグラム
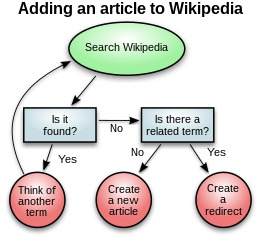
ダイアグラム(diagram)とは、幾何学的な図示を指す。情報を整理し象徴的に表現しモデル化する。
関数などのそれはグラフと呼ぶ。
概要
[編集]「ダイアグラム」という言葉
[編集]「ダイアグラム」という言葉には通常2つの意味がある。
- (広義)視覚情報の表現手段を表す集合名詞。「イラストレーション」のような代表用語として用いられ、グラフやテーブルを含む種類全体を表す。
- (狭義)定性的なデータを表現する特定の視覚表示の種類。線、矢印、その他の視覚的リンクでつながった図形によって表現される。
科学分野では、両方の意味で使われる。例えばマイケル・アンダーソン(Michael Anderson)は、「ダイアグラムとは、絵画であり、さらに言えば抽象絵画であり、また情報の表現でもある。地図、線グラフ、棒グラフ、工学分野の青図、そして建築家・設計士の描く見取図(アイソメ図、アクソメ図)から模式図などまで - これらはすべてダイアグラムである。写真やビデオはダイアグラムではない。」と語っている[1]。他方、リチャード・K・ロウ(Richard K. Lowe)は、ダイアグラムを「それが表現する主題の抽象的なグラフ描画」と定義する。そこにはフローチャート、アイディア図、PERTのような視覚表現だけが含まれる[2]。
「ダイアグラム」という言葉は、「チャートとダイアグラム」(charts and diagrams)というように、しばしば「チャート」(chart)という言葉と一緒に使われる。ダイアグラムは量的な概念よりも質的な概念を表すために使われるが、チャートは量的・質的両方の情報を包含する。「チャートとダイアグラム」という言葉は、質的な情報を伝えるための種類、という説明をする場合に特によく使われる。[3]
特徴
[編集]ダイアグラムとチャートは、情報を直接的に表現するコンピュータグラフィックスや製図などとは対照的に、「抽象的」である[3]。本質的には、ダイアグラムとは、[3]
本質的な意味を伝えるため、ダイアグラムはよく簡略化された図やカリカチュア(ポンチ絵)を使う[2] 。ジャン・V・ホワイト(Jan V. White)によると、良いダイアグラムは、優雅で、明瞭で、平易で、模範的で、簡易で、そして妥当である、という特徴を持つ。ホワイトにとっての優雅さとは、ダイアグラムで表現されたものが、ある問題に対する最も簡潔かつ最も適切な解決策である、ということを意味する[4]。
応用
[編集]ダイアグラムとチャートは、動作・プロセス・事象・概念を表現するのに適している。さらに、視覚を好む多くの人々に対して思考の手助けとなる視覚的手段を提供する。それらは意思決定プロセスにおいて使用される。プログラマにとっては、構造化されたダイアグラムが正確性・迅速な開発・自動確認・関連付け・標準化の手助けとなる[5]。
リー・E・ブラッスール(Lee E. Brasseur)によると、ダイアグラムとは、テキスト付きのドローイング(線画)であり、概念を伝える線および図形から構成される。広義のドローイングは生物や物体の写実的描写を含むが、ダイアグラムは(状況依存の詳細を示すためではなく)抽象的な構造を示すためのドローイングの1種類である。状況や概念の「本質」(essence)に近いものを提供するもの、と考えることができる[3]。
歴史
[編集]マイケル・フレンドリー(Michael Friendly)によると、視覚化(visualization)の必要性は、航海や探検に必要な地図を作成するために作られた、星と他の天体の位置を記した表の中の幾何図形の中で、初めて生じた。それらの起源は有史以前に遡り、各古代文明にはそれぞれ独自の様式があった。16世紀までには、正確な観測および量の計測のための技法や器具が生み出され、視覚化の生まれる土壌となった。17世紀には、大きな理論的進展と実践的応用が見られ、解析幾何学・測定誤差理論・確率論・人口統計・政治算術などが生まれた[6]。
18世紀・19世紀になると、人口や社会・道徳・医療・経済に関する統計が、大規模かつ定期的に取られるようになり、行政計画およびその正当性の検証のためのこれら大量データの有用性が認識され始め、視覚思考がなされるようになった。ダイアグラムは数学的証明と関数を説明するためにも使用され、ノモグラム(nomogram、計算図表)は計算を支援するために生み出された。さらに、収集された数値データの特性を知るために、様々な種類のグラフが発明された。これらにより傾向や分布を簡単に理解・伝達することが可能になり、また視覚検査が可能となった。このうち、円グラフや折れ線グラフ、棒グラフなど主要なグラフはウィリアム・プレイフェアによって生み出された。
統計学(statistics)という言葉は国(state)に由来するが、統計学と地理学の進展により、収集された数値データが地図上で視覚的に表現されるようになった。現在では主題地図(Thematic cartography)と呼ばれている[6]。
主なダイアグラムの種類
[編集]主要な種類(分類)を紹介する。
グラフ・ベースのダイアグラム
[編集]ここで言う「グラフ」は、グラフ (関数) ではなくグラフ理論のほうのグラフである。アイテムの集合およびそれらの関係性を2次元上に位置付けることにより表現する。アイテムの接続または重なりによってその関係が表現される。以下に例を示す。
- 樹形図(tree diagram)
- ネットワーク図(network diagram)
- クラスタ図(cluster diagram)
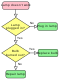
- フローチャート(flowchart)
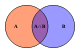
- オイラー図(Euler diagram)、 ベン図(Venn diagram)、 存在グラフ(existential graph)
|
チャート
[編集]離散的または連続的な値の範囲(定義域)において、2つの変数の関係性を示す(日本語では一般的に「グラフ」と呼ばれるものが多い(こちらはグラフ理論ではなくグラフ (関数) の方である))。以下に例を示す。
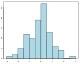
- ヒストグラム(histogram)、 棒グラフ(bar chart)
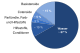
- 円グラフ(pie chart)
- 関数グラフ(function graph)
- 散布図(scatter plot)
- テーブル(table) / 行列(matrix)
|
その他のダイアグラム
[編集]- 交通機関運行表(ダイヤグラム、service planning diagram、いわゆる「ダイヤ」) - 列車ダイヤなど。折れ線チャート状の図表を用いることに由来する名称である。
- 地図(ロンドン地下鉄路線図のように様式化されている場合 - インフォグラフィック)
- 分解組立図(exploded view)
|
他にも多数のダイアグラム技法が存在する。次節ではそのいくつかを紹介する。
様々なダイアグラム
[編集]- A-Z
- Express-G図(Express-G)
- HCPチャート
- HIPO[7](hierarchy plus input-process-output diagram、ハイポ)
- IDEF0 - 実体関連モデルに基づくデータモデリング手法。
- IDEF1X - 実体関連モデルに基づくデータモデリング手法。
- N2チャート
- OBASHI法(Business & IT Diagram (B&IT)) - ビジネスITモデリングで使用される。
- PERT(Program Evaluation and Review Technique)
- SLP(Systematic layout planning、体系的設備配置計画)
- SSADM(Structured Systems Analysis and Design Methodology、構造化システム分析・設計手法) - ソフトウェア工学で使用される。
- TQM図(TQM (Total Quality Management) diagram、総合品質管理図)
- あ行
- アクティビティ図(Activity diagram) used in UML and SysML
- 依存関係図(Dependency diagram)
- イベント駆動型プロセス連鎖(EPC)(Event-driven process chain)
- インターロックブロック図(Internal Block Diagram (IBD)) - SysMLで使用される。
- イーディー=ホフステー図
- インフォグラフィック
- 運動図(Kinematic diagram)
- エマグラム
- オイラー図(Euler diagram)
- オブジェクト図(Object diagram) – UMLダイアグラム。
- か行
- 概念マップ(Concept map)
- 回路図(Circuit diagram)
- 可換図(Commutative diagram)
- 拡張ファンクショナルフローブロック図(Extended Functional Flow Block Diagram (EFFBD))
- 家系図(Family tree)、系図
- カテゴリ理論ダイアグラム
- カルトグラム – 記述したい属性値が面積や距離などに比例するよう変形させた地図。たとえば各国の面積をその国の人口に比例させたものなど。
- カルノーサイクル・グラフ(Carnot cycle graph)
- カルノー図(Karnaugh map)
- ガントチャート(Gantt chart) – タスクやアクティビティのタイミングを表示(プロジェクトマネジメントで使用される)。
- 木 (数学)
- クラス図(Class diagram) – UMLダイアグラム。
- グラフ (関数)
- クロスファンクショナル・フローチャート(Cross-functional flowchart)
- グロトリアン図(Grotrian diagram)
- 系統樹
- コラボレーション図(Collaboration diagram) – UML 1.xダイアグラム。
- コミュニケーション図(Communication diagram) – UML 2.0ダイアグラム。
- コルディア図(Cordier diagram)
- コンター図(Contour diagram、等値線図)
- コンテキスト図(Context diagram)
- コンポーネント図(Component diagram) – UMLダイアグラム
- さ行
- サンキー図(Sankey diagram) - プロセスネットワーク中で量に比例する矢印によって原材料、エネルギー、またはコストのフローを表現する。
- シーケンス図(Sequence diagram) - UMLおよびSysMLで使用される。
- システム構成図
- システムコンテキスト図(System context diagram)
- 実体関連図(ER図)(Entity-Relationship diagram (ERD))
- ジャクソン法(Jackson Structured Programming (JSP))
- 自由体図(Free body diagram)
- SDL/GR(SDL/Graphic Representation) - SDL(Specification and Description Language、仕様記述言語)は計算機科学の形式言語で使用される。
- 状態遷移図(State diagram) - UMLおよびSysMLで使用される。
- シュレイアー・メラー法(Shlaer-Mellor) – ソフトウェア工学で使用される。
- ジョンストン図(Johnston diagram)
- 信号空間図(Constellation diagram、信号点配置図)
- 仕様記述言語
- 実体関連モデル
- 湿り空気線図
- スパイダーチャート(Spider chart、レーダーチャート(Radar chart))
- スミスチャート(Smith chart)
- センテンス図(Sentence diagram) - 自然言語センテンス(文)の文法構造を表現する。
- 相互作用概要図(Interaction Overview diagram) – UMLで利用される。
- 相図(Phase diagram)
- 損益分岐点(Line of balance (LOB))
- た行
- 対戦ダイアグラム
- タイミング図: デジタルタイミング図(Digital Timing Diagram)
- タイミング図: タイミング図(UML Timing Diagram)
- ダブルバブルマップ(Double bubble map) - 教育で使用される。
- 滝グラフ
- データ構造図(Data structure diagram)
- データフロー図(Data flow diagram)
- データベースモデル図(Database model diagram)
- 電位-pH図(Pourbaix diagram)
- 等圧線
- 統一モデリング言語(UML)(Unified Modeling Language) - ソフトウェア工学で使用される。
- 特性要因図(Cause-and-effect diagram, Ishikawa diagram)
- 等高線
- 等深線
- 等値線
- トピックマップ
- ドロネー図
- な行
- ナッシー・シュナイダーマン図(Nassi-Shneiderman diagram、別名:ストラクトグラム(structogram)) – 構造化プログラミングの表現の1つ。
- 二分決定図
- ノモグラム(Nomogram)
- は行
- 配管計装線図(Piping and instrumentation diagram (P&ID))
- 配置図(Deployment diagram) – UMLのダイアグラム
- パッケージ図(Package diagram) - UMLおよびSysMLで使用される。
- バックマン線図(Bachman diagram)
- ハッセ図(Hasse diagram)
- パラメトリック図(Parametric diagram) - SysML
- バリューストリーム・マップ(Value Stream Mapping、価値の流れ図)
- ヒートマップ
- ビジネスプロセスモデリング表記法
- ファインマン図(Feynman diagram)
- ブーチ法(Booch method) – ソフトウェア工学で使用される。
- 複合構造図(Composite structure diagram) – UMLダイアグラム。
- プラント系統線図(Plant Diagram)
- プロセスフロー図(Process Flow diagram (PFD)) – 化学工学で使用される。
- フローチャート
- ブロック図(Block diagram)
- ブロック定義図(Block Definition Diagram (BDD)) - SysMLで使用される。
- ペトリネット(Petri net) – アノテーション付き直接2部グラフとして分散システムの構造を示す。
- ヘインズ=ウルフプロット
- ヘルツシュプルング・ラッセル図
- ベン図(Venn diagram)
- ボロノイ図(Voronoi diagram)
- ま行
- や行
- ら行
- ラインウィーバー=バークプロット
- ラジアル図(Radial Diagram)
- リッチピクチャー(Rich Picture)
- ルイス構造式(Lewis Structures)
- 離散ボロノイ図
- 路線図(ロンドン地下鉄路線図/ロンドン地下鉄に潜む動物たちなど)
- わ行
- ワーニエ・オア図(Warnier-Orr diagram)
出典
[編集]- ^ Michael Anderson (1997). "Introduction to Diagrammatic Reasoning". Retrieved 21 July 2008.
- ^ a b Lowe, Richard K. (1993). “Diagrammatic information: techniques for exploring its mental representation and processing”. Information Design Journal 7 (1): 3–18.
- ^ a b c d Brasseur, Lee E. (2003). Visualizing technical information: a cultural critique. Amityville, N.Y: Baywood Pub. ISBN 0-89503-240-6
- ^ White, Jan V. (1984). Using charts and graphs: 1000 ideas for visual persuasion. New York: Bowker. ISBN 0-8352-1894-5
- ^ Martin, James Lenial; Carma L. McClure (1985). Diagramming techniques for analysts and programmers. Englewood Cliffs, NJ: Prentice-Hall. ISBN 0-13-208794-4
- ^ a b Michael Friendly (2008). "Milestones in the history of thematic cartography, statistical graphics, and data visualization".
- ^ HIPO diagram
参考文献
[編集]- Michael Anderson, Peter Cheng, Volker Haarslev (Eds.) (2000). Theory and Application of Diagrams: First International Conference, Diagrams 2000. Edinburgh, Scotland, UK, September 1-3, 2000. Proceedings.
関連項目
[編集]- 可視化(視覚化)
- 統計図表(チャート)
- ダイアグラム作成ソフトウェア
- グラフ作成ソフト
- 図的推論
- グラフ技法の一覧
- グラフ理論
- 数学的ダイアグラム
- プロット (グラフィックス)
- インフォグラフィック
- ダイアグラムの種類 - 様々なダイアグラムを見ることができる。
- ダイアグラム関連のリソース