コンテンツにスキップ

存在グラフ

出典: フリー百科事典『ウィキペディア（Wikipedia）』

存在グラフ（英: existential graph）は、チャールズ・サンダース・パースが考案した、論理式を視覚的な図として表す記法、またはその図である。パースは1882年に初めて論理グラフについての論文を書き、1914年に死去するまでその手法の研究を続けた。

概要

[編集]

パースは存在グラフとして3種類の体系を提案した。

アルファはベータやガンマに内包される。ベータはガンマには内包されない。

アルファ

[編集]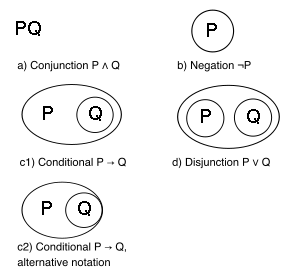
アルファのグラフ

統語論:

  • 空白のページ
  • 字句はページ上の任意の場所に書ける。
  • 任意のグラフを cut または sep と呼ばれる単純な閉曲線で囲むことがある。cut は空でもよい。cut は入れ子や連結は自由だが、交差はできない。

以上のような整形式[1]の部分グラフを「サブグラフ」と呼ぶ。

意味論:

  • 空白ページは「真」を表す。
  • 文字、句、サブグラフ、グラフ全体は、「真」か「偽」のどちらかを表している。
  • サブグラフを cut で囲むことは論理否定を意味するか、ブール代数における補数演算を意味する。従って、空の cut は「偽」を表す。
  • ある cut 内に複数のサブグラフがある場合、それらは暗黙のうちに論理積を表している。

アルファグラフは命題論理の必要最小限の記法であり、論理積と論理否定の表現の妥当性に基づいている。アルファグラフは、二値ブール代数と論理演算を徹底的に単純化したものと見ることもできる。

あるオブジェクトの「深さ(depth)」とは、それを囲んでいる cut の数である。

推論規則:

  • 挿入 - 任意のサブグラフを深さが奇数の位置に挿入できる。
  • 除去 - 深さが偶数の位置にあるサブグラフは除去できる。

同値規則:

  • 二重 cut - 間に何もない二重の cut は、任意のサブグラフを囲んでも意味が変わらない。同様に、間に何もない二重の cut は除去できる。二重否定の除去参照。
  • 反復/非反復 - この規則を理解するには、グラフを木構造として考えた方がわかりやすい。木構造のノード n にあるサブグラフ P は、n から葉の方向の任意のノードにコピーできる。同様に、ノード n にあるサブグラフ P は、そのコピーが n の上位（根方向）にもある場合、除去できる。

証明は、これらの規則を順次適用することでなされる。あるグラフが最終的に空白ページまたは空の cut に還元される場合、そのグラフはいわゆる恒真式（またはその逆）を表している。ある形からそれ以上簡略化できないグラフは、一階述語論理における充足可能な論理式と似ている。

ベータ

[編集]

パースは述語を直観的な英語の語句で記述した。現代の論理学では一般にラテン文字の大文字が使われることが多い。点は、議論領域における何らかの個体の存在を主張するものである。同じオブジェクトの複数のインスタンスは線で結ばれ、これを "line of identity" と呼ぶ。一階述語論理での変項や量化子に相当する記法は存在しない。line of identity で複数の述語を繋いだものは、それら述語が共通の変数を共有していることを意味する。line of identity があるため、アルファグラフにおける同値規則を変更する必要がある。

ベータグラフは、全ての変項が暗黙のうちに量化されるため、全ての論理式が閉じた体系と見ることができる。line of identity の最も浅い部分の深さが偶数であれば、対応する変項は暗黙のうちに存在量化されており、奇数であれば全称量化されている。

Zeman (1964) は、ベータグラフが等号付き一階述語論理と同型であることを初めて指摘した（Zeman 1967 も参照）。しかし、二次文献である Roberts (1973) や Shin (2002) では、同型ではないとしている。パースの著作を見てもこの問題の答えは得られない。というのも、一階述語論理が明確に定式化されたのは彼の死後、1928年のダフィット・ヒルベルトとヴィルヘルム・アッカーマンの Principles of Theoretical Logic が最初だったからである。

ガンマ

[編集]

アルファグラフに、別の種類の閉曲線を追加したものである。その新たな閉曲線は破線で描かれるのが通例である。パースはこれを様相論理の単項作用素のような意味で使った。

Zeman (1964) は、ガンマグラフを素直に改訂すると、様相論理 S4 と S5 になると指摘した。このため、ガンマグラフは正規様相論理の一形態と見なすことができる。Zeman のこの発見は、あまり注目されていない。

パースの役割

[編集]

記号学の先駆者であったパースだが、存在グラフはパースの論理学者/数学者としての業績の中では奇妙なものである。パースの論理グラフは彼の数ある業績の中のごく一部に過ぎない。1867年からの一連の論文と、その集大成とも言うべき1885年の American Journal of Mathematics に掲載された論文で、パースは二値ブール代数、命題計算、量化と一階述語論理、初歩的な集合論といった業績を上げている。モデル理論の先駆者とも言われている。また、オーガスタス・ド・モルガンの relation algebra の拡張も行った。彼はメタ論理学の手前まで研究していた。

しかし、パースは記号学の理論を発展させる過程で、線形（1次元）の記法で論理を定式化する記法を疑問視し、2次元（さらには3次元）で論理や数学を表すことを好むようになった。彼はオイラー図やベン図を進化させた。フレーゲも1879年の Begriffsschrift で論理を2次元で表記しているが、パースのものとはかなり異なる。

パースの論理グラフに関する最初の論文では、アルファ存在グラフと実質的に対をなす体系を提案しており、これを事物グラフ(entitative graph)と呼んだ。しかし間もなく存在グラフを考案すると、事物グラフは捨ててしまった。論理グラフは存命中も注目されることはなく、死後も無視され続けた。評価されるようになったのは、Roberts (1964) と Zeman (1964) からである。

参考文献

[編集]

一次文献

[編集]
  • 1931-35. The Collected Papers of C.S. Peirce. Pp 320-470 of vol. 4. オンライン版として 4.372-417[リンク切れ] と 4.418-529 がある。
  • 1992. Reasoning and the Logic of Things. Ketner, K. L., and Hilary Putnam, eds.. Harvard University Press.
  • 2001. Semiotic and Significs: The Correspondence between C.S. Peirce and Victoria Lady Welby. Hardwick, C.S., ed. Lubbock TX: Texas Tech University Press.
  • A transcription of Peirce's MS 514, edited with commentary by John Sowa.

二次文献

[編集]
  • Hammer, Eric M., 1998, "Semantics for Existential Graphs," Journal of Philosophical Logic 27: 489 - 503.
  • Roberts, Don D., 1964, "Existential Graphs and Natural Deduction" in Moore, E. C., and Robin, R. S., eds., Studies in the Philosophy of C. S. Peirce, 2nd series. Amherst MA: University of Massachusetts Press.
  • --------, 1973. The Existential Graphs of C.S. Peirce. John Benjamins.
  • Shin, Sun-Joo, 2002. The Iconic Logic of Peirce's Graphs. MIT Press.
  • Zeman, J. J., 1964, The Graphical Logic of C.S. Peirce.
  • --------, 1967, "A System of Implicit Quantification," Journal of Symbolic Logic 32: 480-504.

脚注

[編集]
[脚注の使い方]
  1. ^ 英: well-formed

関連項目

[編集]

外部リンク

[編集]
「https://ja.wikipedia.org/w/index.php?title=存在グラフ&oldid=91633873」から取得