プラズマのモデリング

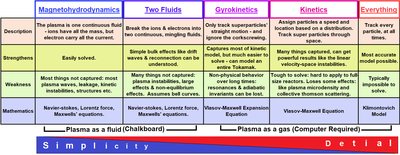
プラズマのモデリング または プラズマのモデル化 とは、プラズマの状態を記述する運動方程式を解く事を指す。電磁場を記述するマクスウェル方程式、もしくは静電場を記述するポアソン方程式も連成して解かれる場合が多い。プラズマは多数の粒子(電子、イオン、電気的中性な分子、ラジカル等)から構成される。それらをモデル化する方法にはいくつかの種類があり、それぞれ利点と制限を持っている^[1]。

試験粒子モデル

試験粒子モデルは、印加された電場(電界)と磁場(磁界)の中を電子とイオンが独立的に動くものとしてプラズマを記述する。ここで電場と磁場は電子やイオンに対して外力として作用し、荷電粒子間の相互作用は考慮されない。そのため、この手法はセルフコンシステントではない。これらの理想的な状態にある電子やイオンは 試験粒子 (テストパーティクル) と呼ばれる^[2]。

試験粒子はローレンツ力に従って旋回運動をするが、多くの場合、比較的速い円運動と旋回中心の比較的遅いドリフトの重ね合わせとして扱うことが可能である。

運動論モデル

運動論モデルは、プラズマを記述する最も基礎的な方法であり、粒子の位置 ${\vec {x}}$ と速度 ${\vec {v}}$ の6次元位相空間 $({\vec {x}},{\vec {v}})$ における 分布関数 $f({\vec {x}},{\vec {v}},t)$ でプラズマを記述する。ここで、位置 ${\vec {x}}$ と速度 ${\vec {v}}$ は独立変数である。分布関数の支配方程式として、次のいずれかが解かれる。

ボルツマン方程式

粒子間相互作用を2体衝突で近似した衝突項 (ボルツマンの衝突項) が置かれる。衝突項には複雑な多重積分が含まれており、近似された衝突モデルかモンテカルロ法が使用される。長距離にまで影響が及ぶクーロン相互作用を衝突項で考慮すると、厳密には不正確となる。そこで、荷電粒子間の相互作用や多体衝突効果を正確に考慮する場合は、集団運動が作る電磁場の作用として扱う^[3]^[4]。

ブラゾフ方程式

ボルツマン方程式において衝突項を0と置いた式である。近距離の粒子間相互作用の影響が小さい系に対して適しており、天体物理学等の分野ではよく使用される。

フォッカー・プランク方程式

衝突による小角散乱をマルコフ過程で扱った衝突項 (フォッカー・プランクの衝突項) が置かれる。この衝突項は輸送現象や緩和現象の扱いに適している。

分布関数より得られる電荷と電流は、マクスウェル方程式を介して電磁場をセルフコンシスタントに定める。

数値シミュレーションを実施する上では、分布関数を6次元位相空間で離散化する必要がある。この離散化には粒子的な手法または連続体的な手法が使用される^[5]^[6]。プラズマ解析に使用される代表的な粒子法にはPIC-MCC法がある^[7]。

ジャイロ運動論モデル

ジャイロ運動論モデルは、粒子の円運動をジャイロ周期に渡って平均化する。このモデルはバックグラウンドに強い磁場を伴う系に対して適切であり、トカマクプラズマが持つ不安定性のシミュレーションに対して広く使用されている^[8]。また最近では天体物理学におけるオーロラ解析等でも利用されている。

流体モデル

運動論モデルはプラズマの物理現象を正確に記述するが、多くの複雑性 (および数値シミュレーションでは多くの計算負荷) を伴う。流体モデルでは 巨視量 (密度、平均速度、平均エネルギー等の、分布関数の速度空間における積率)を基礎変数にしてプラズマを記述することで、計算をより単純にする。これらの巨視量に対する方程式は、いわゆる流体方程式と呼ばれ、運動論的方程式の速度空間における積率を取る事で得られる。

流体方程式は、輸送係数 (移動度や拡散係数等) の定め無しでは閉じられていない。輸送係数を定めるためには、分布関数をいくつかある候補の中から選択して仮定する必要がある。熱平衡が実現している系に対しては、マクスウェル分布は1つの良い選択である。しかし非平衡性が強くなるプラズマの系では、粒子の速度分布がマクスウェル分布から大きく変化する事が知られており、マクスウェル分布を仮定するといくつかの矛盾を抱える事がある^[3]^[4]^[9]^[10]。

流体方程式と電磁場方程式との結合系を考える理論体系は、電磁流体力学として知られている。

運動論と流体のハイブリッドモデル

ハイブリッドモデルでは、系の粒子種のいくつかを流体として、その他を運動論的に扱う。流体で扱う粒子種と運動論的に扱う粒子種、および電磁場がセルフコンシステントに解かれるように構成される必要がある。

プラズマ解析専用のシミュレータ製品

運動論ベース

LSP - www.northropgrumman.com
Magic - www.northropgrumman.com
Particle-PLUS - www.wavefront.co.jp

流体ベース

VizGlow - esgeetech.com
VizSpark - esgeetech.com

また、上記に挙げたプラズマ解析専用のシミュレータの他に、汎用的な流体解析シミュレータにプラズマ解析機能が含まれるものもある。

教科書

Francis F. Chen, 'Introduction to Plasma Physics and Controlled Fusion', 3rd edition, Springer (2015), ISBN 978-3-319-22308-7
Nicholas Krall and Alvin Trivelpiece, 'Principles of Plasma Physics', San Francisco Press (1986), ISBN 978-0-911302-58-5
M. A. Lieberman and A. J. Lichtenberg「プラズマ/プロセスの原理」第2版、堀勝監修、佐藤久明訳、丸善出版 (2010年)、原著 'Principles of Plasma Discharges and Materials Processing'、ISBN 978-4-621-08223-2
宮本健郎「核融合のためのプラズマ物理」『NIFS-PROC-80』シリーズ、核融合科学研究所 (2010年)、ISSN 0915-6348
関口忠「プラズマ工学」『電気学会大学講座』シリーズ、オーム社 (1997年)、ISBN 4-88686-220-9

脚注

^ L. L. Alves et. al. (2018). “Foundations of modelling of nonequilibrium low-temperature plasmas”. Plasma Sources Sci. Technol. 27 (2): 023002. doi:10.1088/1361-6595/aaa86d.
^ 日本機械学会編『原子・分子モデルを用いる数値シミュレーション』7号、コロナ社〈コンピュータアナリシスシリーズ〉、1996年。ISBN 4-339-04141-6。
^ ^a ^b M. A. Lieberman、A. J. Lichtenberg『プラズマ/プロセスの原理』堀勝監修、佐藤久明訳（第2版）、丸善出版、2010年1月（原著2005年）。ISBN 978-4-621-08223-2。
^ ^a ^b 関口忠『プラズマ工学』オーム社〈電気学会大学講座〉、1997年。ISBN 4-88686-220-9。
^ 内藤裕志、佐竹真介「粒子シミュレーションのコーディング技法」『プラズマ・核融合学会誌』第89巻第4号、2013年4月25日、245-260頁、ISSN 09187928、NAID 110009604189。
^ 真壁利明「反応性非平衡プラズマのモデリング」『応用物理学会』第60巻第7号、1991年、663-673頁、CRID 1390001204595199872、doi:10.11470/oubutsu1932.60.663。
^ Birdsall, C.K. (1991). “Particle-in-cell charged-particle simulations, plus Monte Carlo collisions with neutral atoms, PIC-MCC”. IEEE Transactions on Plasma Science 19 (2): 65–85. Bibcode: 1991ITPS...19...65B. doi:10.1109/27.106800. ISSN 0093-3813.
^ 洲鎌英雄「ジャイロ運動論」『プラズマ・核融合学会誌』第79巻第2号、2003年、107-120頁、CRID 1390001206513415552、doi:10.1585/jspf.79.107。
^ J. van Dijk et. al. (2009). “Plasma modelling and numerical simulation”. J. Phys. D: Appl. Phys. 42 (19): 190301. doi:10.1088/0022-3727/42/19/190301.
^ 電気学会・マイクロ波プラズマ調査専門委員会編『マイクロ波プラズマの技術』オーム社、2003年。ISBN 4-274-19710-7。