場の量子論
この記事の正確性に疑問が呈されています。 |
この記事には独自研究が含まれているおそれがあります。 |
この記事は英語版の対応するページを翻訳することにより充実させることができます。(2024年6月) 翻訳前に重要な指示を読むには右にある[表示]をクリックしてください。
|
| 場の量子論 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||
| (ファインマン・ダイアグラム) | ||||||||||||||
| 歴史 | ||||||||||||||
| ||||||||||||||
場の量子論(ばのりょうしろん、英: quantum field theory (QFT))は、量子化された場(素粒子物理ではこれが素粒子そのものに対応する)の性質を扱う理論である。
概要
[編集]量子論の中でも、位置や運動量などの古典力学由来の物理量と、スピンなどの量子論特有の物理量を、基本変数とする量子論を量子力学と呼ぶ。一方、基本変数として「場とその時間微分または共役運動量」を用いる量子論を場の量子論と呼ぶ。量子力学は、場の量子論を低エネルギー状態に限った時の近似形として得られる。現代では、古典的に場であったもの(電磁場など)だけでなく、古典的に粒子とみなされてきた物理系(電子など)の量子論も、場を基本変数にしたほうが良いことがわかっている。[1]
場の量子論には相対論的場の量子論と非相対論的場の量子論がある。相対論的場の量子論は、特殊相対性理論と量子力学の統合を目指すものである。非相対論的場の量子論は、相対論的場の量子論の非相対論的極限、すなわち光速を無限大とする極限とみなされる。[2]
場の量子論は、高エネルギーの系や、凝縮系(多体系)を記述する。相対論的な場の量子論は特殊相対論的要請を満たす形式を備え、量子力学と特殊相対性理論の両方を満足する。素粒子物理、原子核物理学や物性物理といった領域で、基礎理論として用いられる。
- 素粒子物理学
- 素粒子の振る舞いを記述するのに用いられる。素粒子が反応し新たな素粒子となる現象はその一例である。量子電磁力学、ワインバーグ・サラム理論、量子色力学といった、実験によって検証されている理論や、弦理論等の仮説上の理論が、場の量子論を基礎として研究されている。
- 物性物理学
- 非相対論的な場の量子論が用いられることも多く、臨界現象・相転移などの多体論的効果を記述する。超伝導のBCS理論、量子相転移といった物理が、場の量子論の文脈により理解される。
摂動的場の量子論では、粒子の間に働く力は、力を伝える粒子の交換により生じる。例として電子の間に働く電磁力は、光子の交換により生じる。同様に、ウィークボソンは弱い力を媒介し、グルーオンは強い力を媒介する。
力を媒介するのと同じ場の励起である光子が、塊状の波として電磁波となり、またナノスケールの現象においては粒子のように振舞う。電子も同様で、対応した場の励起として表される。このように、古典物理での粒子と場は、場の量子論により粒子と場の2重性を持つ形式に書き改められる。
場と粒子
[編集]場は時空間のあらゆるところで定義され、波動を引き起こす能力がある[3]。空間全域に広がる場がエネルギーを得て振動すると、粒子のように振る舞う[4]。現代物理学における粒子とは、エネルギーが局在化している状態[5](波束)、または場に付随するエネルギー量子[3]のことである。
場の量子論ではこのように粒子を広く捉えることで、以下のような特徴[3]を持つ粒子を場の立場から考えている。
- 各瞬間で局在しており、数えられる。
- 生成・消滅し、粒子数は変化する。粒子は必ずしも安定ではない。
- 1個の粒子はスピンを持つ。
- 物質を構成する粒子と力を伝達する粒子の2種類に分けられる。
- 反粒子が存在する。
成立史
[編集]背景
[編集]ジェームズ・クラーク・マクスウェルの古典電磁気学では、粒子(荷電粒子)が場(電磁場)を生み、場が粒子に力を与える。これは、場の理論の最初の定式化である。
原型
[編集]1927年から1928年、ポール・ディラックによる古典電磁気学の量子化、オスカル・クライン、パスクアル・ヨルダン、ユージン・ウィグナーおよびウラジミール・フォックによる生成消滅演算子が形成され、場の量子論の原型をヴェルナー・ハイゼンベルクとヴォルフガング・パウリが創った。
ハイゼンベルクは、場において粒子が力を伝えるという見解を打ち出した。これが湯川の強い力(中間子)、フェルミの弱い力(電子)の元となる。しかし、湯川が提唱した強い力のモデルに対しては、ハイゼンベルクやボーアは否定的であった。
相対論的共変・繰り込み
[編集]ハイゼンベルクおよびパウリらが作った原型は相対論を満たすが、相対論的共変形式を満たさなかった。1943年、朝永振一郎が超多時間理論でこれを解決する。これは1932年にポール・ディラックが提唱した多時間理論(相互作用をしている電子一つ一つに独立な時間を与える)の電子の生成・消滅を含まないという欠点を改めたものである。また、リチャード・ファインマンも経路積分を完成し、またジュリアン・シュウィンガーもこの問題を独立に解決する。
ゲージ理論
[編集]ゲージ理論の概念は、1918年のヘルマン・ワイルのアイデアに端を発する。ワイルは時空点ごとに「ゲージ」(ものさし)を与え、時空点が変わっても理論が変わらないようラグランジアンを決める(ゲージは一種の自由度で、理論不変なようにゲージ自由度を与える)ことを要求し、電磁場の導出を試みたが、実験と合わなかった。1927年、フリッツ・ロンドンは、長さを位相に変え、ゲージ理論の有効性を証明した。
1954年、楊振寧およびロバート・ミルズはゲージ対称性を非アーベル群に拡張した理論を定式化した(非可換ゲージ理論)。(ヴォルフガング・パウリ、内山龍雄も独立して同様の理論を発見している。発表が遅れたため、パウリや内山らは非可換ゲージ理論の発見者と見なされない。)内山龍雄は重力場を含む形に拡張した(このため、ヤン=ミルズ=内山理論と呼ぶ人もいる)。この非可換ゲージ理論は、後に量子色力学やワインバーグ=サラム理論を定式化する際に用いられた。
クォーク模型
[編集]1964年、マレー・ゲルマン、ユヴァル・ネーマンおよびジョージ・ツワイクにより独立にクォーク模型が見出された。この原型は坂田昌一による坂田模型と、そのフレーバー変換を群論形式で記述する方法を確立した大貫義郎らによるIOO理論SU(3)である。(これはクォーク模型の原型における対称性を群論で記述した最初の事例であり、素粒子論の核で群論を使う以後の流れを決定づける。
量子力学での群論の最初は、ヘルマン・ワイル1927年である。原子スペクトルの対称性を記述[6]。また、1939年、ユージン・ウィグナーが原子核をSU(4) で記述する[7]。しかしこれは素粒子論の核での使用ではなかった。これらは、素粒子の基本構造に迫るものではなく、素粒子研究で注目を浴びなかった。
自発的対称性の破れ
[編集]ゲージ理論では、ゲージ対称性を満たす場合、必然的にゲージ場の質量がゼロになる。しかし、光子を除く現実の粒子は質量を持ち、質量が力の及ぶ範囲を決める。1964年、これを救ったのが、ピーター・ヒッグスらのヒッグス機構で、南部陽一郎の自発的対称性の破れを使い解決した。
自発的対称性の破れの概念は、ハイゼンベルクが強磁性体モデルにおけるスピンのSU(2)回転対称性について論じたのが始まりとされる。1960年に南部は、超伝導のBCS理論をヒントに対称性の自発的破れの概念を場の量子論において定式化した。[8][9]。
量子色力学・ワインバーグサラム理論
[編集]量子電磁力学 (QED) は可換ゲージ理論である。一方、量子色力学 (QCD) およびワインバーグ=サラム理論は非可換ゲージ理論である。量子色力学は3つの場のからみ合いであり、ゲージも3×3の行列となり、QEDの可換ゲージから、非可換ゲージにかわる。
弱い力と電磁相互作用は、1967年、場の量子論の枠組みで非可換ゲージ形式のワインバーグ=サラム理論により統一される。
強い力は、クォーク模型の完成後、1971年にヘーラルト・トホーフトの非可換ゲージの繰り込み可能性の証明を経て、1973年に繰り込み群を使ったデイビッド・グロスらによって場の量子論の枠組みで非可換ゲージ形式の量子色力学 (QCD) が完成する。
理論の詳細
[編集]この節の加筆が望まれています。 |
場の量子化
[編集]量子力学では古典的に書き下した運動方程式を元に、位置や運動量を非可換な行列ないしは演算子と考える事で、量子論の描像を得る。これを正準量子化と呼ぶ。場の量子論では同様の方法を、場という物理量に対し適用する。これにより、時空間上の位置をパラメーターとして持つ場の演算子が得られる。
特に自由場の理論(場同士が一切相互作用しない理論)において、この方法で定義された演算子の各振動数モードは、独立した調和振動子とみなす事ができる。この系の量子的なふるまいは生成消滅演算子によって記述される。
摂動論と繰り込み
[編集]正準量子化によって厳密な場の時間発展を記述できるのは、自由場など少数の例に限定される。量子電磁力学のような複雑な理論を扱うには通常、摂動論の考え方を用いる。これは相互作用描像などを用いて、相互作用のある場の時間発展を自由場の演算子の積に展開する方法である。
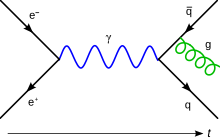
場の量子論における演算子積の計算は、仮想粒子を含む多数の項を、運動量保存や対称性などを考慮してまとめあげる、かなり煩雑なものとなる。これを視覚的に表すツールとしてファインマンダイアグラムがある。
また、摂動計算では仮想粒子の取りうる運動量すべてを積分する必要があり、これによって計算結果が無限大に発散する紫外発散の問題が起こる。この問題への処方として繰り込みが用いられる。
非摂動論的な方法
[編集]摂動論は相互作用が弱い事を仮定した議論であり、結合定数の強い領域には上手く適用できない。特に量子色力学の低エネルギー領域における、カイラル対称性の破れなどの物理については摂動論を用いては扱うことができない。そのため並行して、以下のような非摂動論的方法が用いられる。
脚注
[編集]- ^ 清水明『新版 量子論の基礎―その本質のやさしい理解のために―』サイエンス社、2004年。ISBN 4-7819-1062-9。
- ^ 新井朝雄「場の量子論の数理 : Mathematical Aspects of Quantum Field Theory」応用物理, Vol3, No.4, P.292-306 (1993).
- ^ a b c 長島順清『素粒子物理学の基礎I』朝倉書店〈朝倉物理学大系〉、2002年。ISBN 4-254-13673-0。
- ^ 吉田伸夫『素粒子論はなぜわかりにくいのか~場の考え方を理解する』技術評論社、2013年。ISBN 978-4774161310。
- ^ 坂本眞人『場の量子論-普遍性と自由場を中心として-』裳華房〈量子力学選書〉、2014年。ISBN 978-4785325114。
- ^ Wigner Biography Archived 2011年9月23日, at the Wayback Machine.
- ^ Ann. of Math. (2) 40 (1939), 149-204
- ^ 南部理論と物性物理学
- ^ Symmetry and Symmetry Breaking
関連図書
[編集]- 高橋康:「物性研究者のための場の量子論」IおよびII、培風館(1974).
- 中西襄:「場の量子論」、培風館(1975年).
- Claude Itzykson and Jean-Bernard Zuber: Quantum Field Theory, Mc.Graw Hill, ISBN 0-07-066353-X (1985).
- 崎田文二、吉川圭二:「経路積分による 多自由度の量子力学」、岩波書店、ISBN 4-00-005313-2 (1986年8月29日).
- 西島和彦:「場の理論」、紀伊國屋書店(1987年).
- 江沢洋、新井朝雄:「場の量子論と統計力学」、日本評論社、ISBN 4-535-78163-X (1988年6月25日)
- Giorgio Parisi:「場の理論:統計論的アプローチ」、吉岡書店、ISBN 4-8427-0245-1(1993年4月25日).
- 中西襄:「ファインマン・ダイアグラム」、丸善株式会社、ISBN 4-621-03852-4 (1993年6月30日).
- 大貫義郎:「場の量子論」、岩波書店、ISBN 4-00-010435-7 (1994年6月8日).
- 永長直人:「物性論における 場の量子論」、岩波書店、ISBN 4-00-005934-3 (1995年10月27日).
- 高橋康:「多量子問題から場の量子論へ」、講談社サイエンティフィク、ISBN 4-06-155101-9 (1997年3月10日).
- Alexandre M. Zagoskin: Quantum Theory of Many-Body Systems, Springer-Verlag (1998).
- A.N.カマール:「場の量子計算入門」、講談社サイエンティフィク、ISBN 978-4-06-153229-8 (1998年4月10日).
- A.M.ザゴスキン:「多体系の量子論<技法と応用>」、シュプリンガー・フェアラーク東京、ISBN 4-431-70832-4 (1999年6月26日).
- 村井信行:「拘束系の力学」、日本評論社、ISBN 978-4-535-78249-5 (1998年6月10日).
- 永長直人:「電子相関における場の量子論」、岩波書店、ISBN 4-00-005701-4 (1998年10月8日).
- Michael Stone: The Physics of Quantum Fields, Springer-Verlag (2000).
- 新井朝雄:「フォック空間と量子場[上]」、日本評論社、ISBN 4-535-78317-9 (2000年8月10日).
- 新井朝雄:「フォック空間と量子場[下]」、日本評論社、ISBN 4-535-78318-7 (2000年8月10日).
- M.ストーン:「量子場の物理」、シュプリンガー・フェアラーク東京、ISBN 4-431-70940-1 (2002年2月2日).
- 新井朝雄:「多体系と量子場」、岩波書店、ISBN 4-00-011113-2 (2002年2月15日).
- 山田耕作:「凝縮系における場の理論:フェルミ液体から超伝導へ」、岩波書店、ISBN 4-00-011121-3 (2002年6月20日).
- 坂井典佑:「場の量子論」、裳華房、ISBN 4-7853-2212-8 (2002年11月20日).
- 石川健三:「場の量子力学」、培風館、ISBN 4-563-02389-2 (2006年7月20日).
- Alexander Altland and Ben Simons: Condensed Matter Field Theory, Cambrdige University Press, ISBN 978-0-521-84508-3 (2006).
- 江澤潤一:「量子場の理論:素粒子物理から凝縮系物理まで」、朝倉書店、ISBN 978-4-254-13775-0 (2008年7月5日).
- 日置善郎:「相対論的量子場:演算子の基礎的性質」、吉岡書店、ISBN 978-4-8427-0346-6 (2008年10月15日).
- V.P.ナイア:「現代的な視点からの 場の量子論[基礎編]」、シュプリンガー・ジャパン、ISBN 978-4-431-10073-7 (2009年12月6日).
- V.P.ナイア:「現代的な視点からの 場の量子論[発展編]」、シュプリンガー・ジャパン、ISBN 978-4-431-10074-4 (2009年12月6日).
- Alexander Altland、Ben Simons:「凝縮系物理における場の理論(上)」、吉岡書店、ISBN 978-4-8427-0352-7 (2009年11月15日).
- Alexander Altland、Ben Simons:「凝縮系物理における場の理論(中)」、吉岡書店、ISBN 978-4-8427-0354-1 (2010年1月15日).
- Alexander Altland、Ben Simons:「凝縮系物理における場の理論(下)」、吉岡書店、ISBN 978-4-8427-0356-5 (2010年5月20日).
- F.マンドル、G.ショー:「場の量子論:第1巻、量子電磁力学」、丸善出版、ISBN 978-4-86345-081-3 (2011年5月20日).
- 川村嘉春:「相対論的量子力学」、裳華房、ISBN 978-4-7853-2510-7 (2012年10月25日).
- A.M.ザゴスキン:「ザゴスキン 多体系の量子論[新装版]」、丸善出版、ISBN 978-4-86345-144-5 (2012年11月25日).
- 坂本眞人:「場の量子論:不変性と自由場を中心にして」、裳華房、ISBN 978-4-7853-2511-4 (2014年11月5日).
- 磯暁:「現代物理学の基礎としての 場の量子論」、共立出版、ISBN 978-4-320-03487-7 (2015年6月25日).
- 藪博之:「多粒子系の量子論」、裳華房、ISBN 978-4-7853-2514-5 (2016年11月15日).
- Anthony Zee(著)、原田恒司、筒井泉(共訳):「ジー先生の場の量子論:基礎編」、丸善出版、ISBN 978-4-621-30493-8 (2020年1月).
- 坂本眞人:「場の量子論(II): ファインマン・グラフとくりこみを中心にして」、裳華房、ISBN 978-4-7853-2512-1 (2020年9月25日).
- Anthony Zee(著)、原田恒司、筒井泉(共訳):「ジー先生の場の量子論:応用編」、丸善出版、ISBN 978-4-621-310330-5 (2025年1月10日).
