表面科学
表面科学(ひょうめんかがく、英語:surface science)は表面または界面を扱う自然科学の一分野のこと。理論、実験両面から様々な研究が行われている。物理学を重視した表面科学を特に表面物理学(surface physics)、化学を重視した表面科学を特に表面化学(surface chemistry)という。
物質の表面は、物質の吸着と脱離、電子的な不安定さ等によって測定することが難しい状態であった。実際に表面の構造が確認できるようになったのは、1950年代に高真空状態にすることで、表面に余計な原子・分子などが付着していない洗浄度を確保できるようになってからである[4][5]。
表面科学の複雑さから、ノーベル物理学賞受賞者のヴォルフガング・パウリは「固体は神がつくりたもうたが、表面は悪魔がつくった」と言い残している[6][7][8]。
概要
[編集]固体の表面を構成する原子は、固体内部(バルク、英語:bulk)を構成する原子よりもはるかに数が少ないため、その影響は少ないだろうと見積もられていた。しかし19世紀後半、ポール・サバティエにより不均一触媒の表面が研究され、さらにアーヴィング・ラングミュアにより物質吸着の研究が進められた結果、固体が外部とエネルギーや物質をやり取りする場としての、表面の重要性が明らかになった。20世紀後半には、表面を原子・分子レベルで観察する手法が開発された。これを用いてゲルハルト・エルトルは表面での化学反応を詳細に研究し、「固体表面での化学過程の研究」の功績で2007年にノーベル化学賞を受賞している[9]。
固体物理学ではx、y、z方向へに無限に続く完全結晶を理想的なモデルとして用いているため3方向の並進対称性を仮定できる。しかし、表面または界面がある場合、系の表面に垂直な方向での対称性が破れる。このため表面や界面に特有の現象、例えば電子の表面準位の発生や原子配列の表面再構成などが起こる。また外から飛来した分子は表面に物理吸着あるいは化学吸着する。特に不均一触媒の表面では、吸着した分子の状態が変化し、分子単独では持っていなかったような反応性を得ることもある。
結晶の表面
[編集]全く同じ物質の表面でも、結晶を切断する面の方向によってその性質は異なる。結晶面はミラー指数によって指定される。例えばSiの単結晶を、ミラー指数が(111)となる格子面に沿って切断した切断面はSi(111)面と呼ばれる。同じSi結晶の表面でも(100)面と(111)面のように、方向が異なれば異なる表面として扱う。固体には並進対称性があるため、整数 k、l、mと単位格子ベクトルa、b、cを用いて、任意の格子点は ka + lb + mcと記述できる。このうちc軸方向を法線とした表面上の格子点は、ka + lbと表せる。すなわち、c軸に垂直な表面はaとbが張る四角形を単位胞とする2次元格子からなる。
バルクの断面と同じ構造の表面を理想表面という。Si(100)面とSi(001)面は方向が異なるが、立方晶であるバルクの対称性がそのまま保たれるとすれば、どちらの断面も等価である。等価な結晶面の集合は、ミラー指数を中括弧で囲んで{100}のように示す。実際の表面が2次元の結晶となっていることは、低速電子線回折 (LEED)、走査型トンネル顕微鏡 (STM)、原子間力顕微鏡 (AFM) などにより確認できる。
理想表面と実際の表面で完全に構造が一致することはまれで、多くの表面では電荷密度の偏りやダングリングボンドに起因する不安定性を緩和するために、原子が理想表面での位置からずれる。このような構造の変化を表面再構成(または再配列)と呼ぶ。表面に吸着した原子や分子が原因で表面再構成が起こることもある[10]。
実際の表面の単位格子ベクトルは、理想表面の単位格子ベクトルの線型結合で表現する。このときの係数を指定すれば、再構成の有無にかかわらず表面の対称性を表現できる。実際には(2×2の行列となる)係数そのものよりも、簡略化したウッドの記法に基づいて「Si(111)-(7×7)」のように表面の対称性を表すことが多い[11]。
主な研究手段
[編集]表面科学の実験には原理的に避けがたい課題がいくつかある。表面の原子はバルクの原子よりも圧倒的に少ないため、通常の分析手法では表面の信号はバルクの信号に埋もれてしまう[12]。したがって表面の分析を行うためには、表面の信号だけを選択的に測定できるような手法を用いる必要がある。また大気圧下では、気体分子が表面に衝突、吸着、脱離を繰り返しているため、分析対象である表面の状態が測定中にも絶え間なく変化してしまう[12]。そのため実験を超高真空下で、気体分子の量や種類をコントロールして行うことも多い。
固体表面の構造を分析するために、走査型トンネル顕微鏡[13]、原子間力顕微鏡[14]、電子回折[15]、X線回折、透過型電子顕微鏡[16]、走査型電子顕微鏡などが用いられる。また組成を分析するために光電子分光やオージェ電子分光などが用いられる[17]。吸着分子の分析には、上記の方法に加えてケルビンプローブによる仕事関数の測定や各種の振動分光、脱離した分子の質量分析などが行われる。
理論面からの研究にも表面科学に特有の課題がある。表面系のバンド計算や構造最適化では、バルクにも用いられる第一原理計算パッケージが流用される。こういったパッケージでは、実空間法などの例外を除いて、x、y、z方向への周期性が計算の前提となっている。しかし表面では法線方向への周期性が崩れているため、そのままでは計算ができない。そのため、表面のある固体を交互に並んだ原子層と真空層で近似して、法線方向の周期性をモデル系に持たせる近似がよく用いられる(スラブ近似)[18]。また表面-分子系を解析するために、巨大なクラスターの端面として表面をモデル化する場合もある(クラスター模型)[19]。
最近の研究動向
[編集]最近では、ナノテクノロジーブームから、ナノ材料と言われる機能材料の開発に力点がシフトしている。例えば、スピントロニクスや、新しい触媒等の開発を目的に掲げているケースが多い。
そのほか、MOSFET用の絶縁体の開発に関係して、絶縁体表面の研究も盛んである。特にシリコン表面にハフニウム酸化物を薄膜として生成させた系は、誘電率の高いゲート絶縁膜として盛んに研究されている。こうした絶縁膜はhigh-k絶縁膜とも呼ばれ、半導体メーカー各社が熾烈な開発競争を展開している。ハフニウムを用いたhigh-k絶縁膜は、従来のシリコン絶縁膜よりも大幅なトンネル電流の削減に成功しており、これを用いた半導体チップも製造されている。
表面分析手法
[編集]- 光電子分光
- 電子回折
- 電子エネルギー損失分光 (EELS)
- ラザフォード後方散乱分光 (RBS)
- イオン散乱分光 (ISS)
- 二次イオン質量分析法 (SIMS)
- 二面偏波式干渉計 (DPI)
- 表面増強ラマン散乱 (SERS)
- 和周波発生 (SFG)
- 走査型プローブ顕微鏡 (SPM)
- 走査型トンネル顕微鏡 (STM)
- 原子間力顕微鏡 (AFM)
参考文献
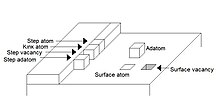
[編集]- ^ FIGURE 1. The terrace-step-kink (TSK) model of a thin-film surface.(ネイチャー)
- ^ 表面拡散場中での原子ステップの不安定化(名古屋大学)
- ^ 結晶表面に見られる魔法数
- ^ 齊藤芳男、「真空排気と水」 『Journal of the Vacuum Society of Japan』 2010年 53巻 9号 p.511-514, doi:10.3131/jvsj2.53.511, 日本真空学会
- ^ 実験化学講座〈24〉表面・界面 序文 ISBN 4621073230
- ^ 表面化学(九州大学 先導物質化学研究所 高原研究室)
- ^ 表面科学ってなんだ(国立研究開発法人産業技術総合研究所)
- ^ As quoted in Growth, Dissolution, and Pattern Formation in Geosystems (1999) by Bjørn Jamtveit and Paul Meakin, p. 291
- ^ "The Nobel Prize in Chemistry 2007" (Press release). Royal Swedish Academy of Sciences. 10 October 2007.
- ^ Niehus, H. (July 1983). “Surface reconstruction of Cu (111) upon oxygen adsorption”. Surface Science 130 (1): 41-49. doi:10.1016/0039-6028(83)90258-3.
- ^ 川合眞紀・堂免一成 『表面科学・触媒科学への展開』 (岡崎廉治 他編 『岩波講座現代化学への入門』 14巻) 岩波書店、2003年
- ^ a b Zangwill, Andrew (1988). Physics at surfaces. New York, NY, USA: Cambridge University Press. p. 20. ISBN 0521347521
- ^ Hasegawa, Y.; Ph. Avouris (December 1992). “Manipulation of the Reconstruction of the Au(111) Surface with the STM”. Science 258 (5089): 1763-1765. doi:10.1126/science.258.5089.1763.
- ^ 森田, 清三、et al.「原子間力顕微鏡によるSiとGe表面での原子操作」『表面科学』第26巻第6号、2005年、351-356頁。
- ^ NOONAN, J. R.; H. L. DAVIS (October 1986). “Atomic Arrangements at Metal Surfaces”. Science 17: 310-316. doi:10.1126/science.234.4774.310.
- ^ Yu, Qingkai; et al. (May 2011). “Control and characterization of individual grains and grain boundaries in graphene grown by chemical vapour deposition”. NATURE MATERIALS 10: 443-449. doi:10.1038/nmat3010.
- ^ Rodriguez, Jose A.; D. Wayne Goodman (August 1992). “The Nature of the Metal-Metal Bond in Bimetallic Surfaces”. Science 14: 897-903. doi:10.1126/science.257.5072.897.
- ^ 小林 一昭「(第一原理)バンド計算と実験との距離」『表面科学』第28巻第3号、2007年、129-134頁。
- ^ 中井 浩巳「表面-分子相互作用系の量子化学計算に関する最近の動向」『表面科学』第28巻第3号、2007年、150-159頁。
