無作為抽出

無作為抽出(むさくいちゅうしゅつ)やランダム・サンプリング(英: random sampling)とは、ある集団から標本(サンプル)を無作為(ランダム)に抽出(サンプリング)する行為のことである。日本工業規格では、「無作為標本」の項で、「無作為な選択方法によって選んだ標本」と定義している[1]。
概要
[編集]

その名の通り、ある集団から要素を抽出するのに、作為的な手順を使わないことが特徴である。そのため、無作為抽出法によるサンプリングを行うと、集団の全ての要素が同じ確率で抽出されることになる。
標本調査における標本の抽出法には、全体から無作為に抽出する「無作為抽出」の他に、全体から作為的に抽出する「有意抽出」がある。例えばクラスの掃除当番を選ぶ場合、「出席簿からくじで無作為に抽出した出席番号の生徒を掃除当番に任命する」のが無作為抽出で、「先生が気に入った奴を掃除当番に任命する」のが有意抽出である。無作為抽出の方が客観的な公平性が担保でき、「段ボールで自作したルーレット」や「印刷に失敗したプリント用紙の裏紙で自作した抽選箱」など割と簡単に道具を作れるので、民間でも割とカジュアルに行われている。仮に「無作為抽出」と称していても、客観的な無作為性が担保できない場合、例えば「出席簿でたまたま目についた奴を何名か無作為に掃除当番に任命する」などは、先生が気に入った奴を有意抽出している可能性が客観的に排除できないので、無作為抽出ではない。
統計調査にも使われる。「割りばしで自作したので特定の番号の物がいつもささくれで引っかかる抽選機」などの精度の低い乱数発生器を使用したことによる無作為性(ランダムネス)の低さは、「掃除当番を選ぶ」などの場合は単に「クジ運が悪い」として我慢してもらえば問題にならないものの(それでも限度があり、あまり悪いと有意抽出と同様にクジ運ではなく先生が恨まれることになる)、統計調査などの学術的調査では標本誤差の元となるので、問題となる。「有意抽出」や、「無作為性の低い無作為抽出」では、正確な統計調査にならない。なので、統計調査として行われる標本調査では、有意抽出ではなく、かならず無作為抽出が使われる。また、人力で調査を行うことによるコストや労力との兼ね合いを取りながら、なるべく無作為性が高くなるように様々な手法が工夫されている。
工業製品の「抜き取り検査」でも、無作為性が低いと不良品の率が正確に解らず、自社検査にパスしたのに出荷先の検査で段ボールの底の方から不良品が大量に見つかって会社の信用がピンチになるので、たとえコストがかかっても無作為性を確保することは重要である。特に、倉庫や段ボールの奥の方に積まれたものを検査するのがマンパワー的に難しく、完全な無作為抽出をせずに上の方だけ適当に検査する事があるので、製品全体の無作為抽出が楽にできるような工夫が必要である。
カードゲームなどのテーブルゲームでも、無作為抽出であることは重要である。ゲームで無作為抽出のように見せかけて自分の欲しい手札を引く「イカサマ」と言うテクニックがある。アナログのゲームにおける無作為抽出は、コンピューターゲームとは違ってコンピューターを使った無作為抽出を行わず、全て人力で行うことが特徴なので、その分イカサマがしやすいが、絶対に行ってはいけない。
手品でも、タネも仕掛けもない無作為抽出であることが強調されるが、実はタネも仕掛けも仕込まれているので無作為抽出ではない。
無作為抽出の手法
[編集]乱数生成器(ランダマイザー)
[編集]

直接、ある集団の全ての要素を無作為に配列(ランダマイズ)し、そこから任意の要素を抽出する方法と、まず、ある集団の全ての要素で構成される任意の配列のリスト(標本抽出枠)を作り、標本抽出枠のそれぞれの要素に連番を振り、乱数生成器(ランダマイザー)で無作為な乱数を生成し、出て来た乱数と同じ番号が振られた要素を標本として標本抽出枠から抽出する方法がある。
例えばトランプや抽選機では、ランダマイズされたものから任意のカードやボールを引くことによって無作為抽出が行われる。トランプではシャッフル、抽選機では回転(俗にガラガラと言う)によってランダマイズが行われる。一方、統計調査などで、人間を無作為抽出する場合は、複数人の人間をまとめてシャッフルできる巨大生物でもない限り、まず調査対象となったある集団(母集団)の全ての人間がリストアップされて連番が降られた標本抽出枠を作って、そこから乱数発生器で乱数を生成して要素を無作為に選んで抽出する方法が使われる。
コンピューターやサイコロなど、要素を無作為に配列したり乱数を発生させたりする装置のことを乱数生成器(ランダマイザー)と言う。カードやボールを人間が自分の手で直接ランダマイズして抽出する場合もあるが、カードやボールをランダマイズせずにあくまで標本抽出枠として使い、サイコロやルーレットなどのランダマイザーで生成した数字をもとに抽出することも多い。テーブルトークRPGやボードゲームでプレーヤーや次のアクションなどを無作為抽出する場合は、ランダマイザーとして「多面ダイス」と言う特殊なサイコロが使われることがある。身近なランダマイザーとしてはコイントスがあり、ボードゲームではかなり使われるが、「0(表)」と「1(裏)」しか生成できないので、標本調査や抜き取り検査では普通は使わない。標本調査や抜き取り検査での無作為抽出におけるランダマイズはコンピューターを使うのが普通だが、コンピューターを使わないボードゲームではアナログのランダマイザーを使うのが普通である。現代では100円ショップでランダマイザー(ダイス、サイコロ、ルーレットなど)が購入できるほか、ホビーショップでもテーブルトークRPG用の様々な多面ダイスが安価に購入できる。
抽選機や全自動麻雀卓など、「ランダマイザー」が無作為抽出におけるランダマイズから抽出までの一連の作業を同時に行ってくれる場合もある。
非復元抽出と復元抽出
[編集]無作為抽出を何度か繰り返して行う場合、既に抽出された要素を母集団から除外して無作為抽出を行う「非復元抽出」と、抽出された要素を除外せずに再び母集団に戻して無作為抽出を行う「復元抽出」がある。
例えばクラスの生徒から掃除当番を決める無作為抽出において「復元抽出」を行った場合、同じ人が何度も繰り返して掃除当番に選ばれる可能性が有り、不都合が生じるので、なるべく「非復元抽出」を行うことが望ましいが、例えばサイコロで無作為抽出を行う場合、既に出た出目が再び出る可能性を原理的に排除できないなど、「非復元抽出」を行うのが難しい場合がある。また、母集団が非常に大きく、抽出される要素数が非常に少ない場合、同じ人が何度も繰り返して抽出される可能性は非常に小さいので、無視されることがあり、「復元抽出」がしばしば使われる。
統計調査における無作為抽出
[編集]統計調査として行われる標本調査における無作為抽出とは、ある調査対象の全体(母集団)から調査対象となる標本を無作為に抽出する行為のことである。標本調査の基本となる手法である。統計調査には「標本調査」の他に、母集団の全数を調査する「全数調査」があるが、母集団が大きかった場合は全数を調査すると費用や手間なども大きくなるため、標本調査が行われる。
無作為抽出を行なえば、統計学の見地に照らし合わせて、標本調査の結果から母集団における平均値や比率などが推定出来る。また、母集団からの無作為抽出は、完全に確率的に現れると言えるので、同じく統計学の見地に照らし合わせて、母集団の推定値(=母数)の誤差の大きさを見積もる事が出来る。
推測統計学を創始したとされるR.A.フィッシャーは、イギリスの農事試験所に14年間勤め、この時期に分散分析法を完成させた。差の有無などの検証にも無作為抽出が理論的前提となった様々な手法が使われる。
統計調査における無作為抽出の手法
[編集]統計調査における無作為抽出の手法は、母集団の全ての要素を対象として単純に無作為抽出を行う単純無作為抽出が最も基本的な方法だが、標本抽出枠が大きかった場合は費用や手間なども大きくなるため、人間が人力で標本調査を行う上で、単純無作為抽出法を使うのは難しい場合も多い。また、単純無作為抽出法では、隣り合った要素同士が選ばれたり、3個以上連続した要素が選ばれる可能性が有るため、例えば市内の高校生の代表を何名か無作為抽出する場合、ワルばかりいる高校の生徒を連続してサンプリングしてしまう可能性が有るなど、標本の精度が悪くなる(標本誤差が大きくなる)恐れがある。
そのため、「単純無作為抽出法」よりも手間や費用が少なくなるような、あるいは「単純無作為抽出法」よりも標本の精度が高くなる(標本誤差が少なくなる)ような、様々な手法が存在する。主な方法としては、系統抽出法、層化抽出法、確率比例抽出法、多段抽出法などがある。どのような方法を取っても、最終的に全ての要素で抽出される確率が同じなら、無作為抽出である。逆に言うと、たとえ自分では無作為に抽出したつもりでも、最終的に各要素・層・クラスター(集団)ごとで抽出される確率にばらつきがあれば、それは無作為抽出ではない。
現実的な調査では、いくつかの無作為抽出法を組み合わせたり、無作為抽出による標本調査と全数調査を組み合わせて使われることも多い。
標本抽出枠と乱数の生成
[編集]統計調査における無作為抽出の前提として、まず母集団から無作為抽出するための「標本抽出枠」(sampling frame)を用意する必要がある。いわば母集団を代表する要素が記述された「リスト」が用意されていないと、そこから無作為抽出を行うことが出来ない。既に用意されている場合もあり、例えば学校では標本抽出枠としてクラスの名簿を使うことが出来る。日本の世論調査では、標本抽出枠として自治体が制作した住民基本台帳などが用いられるが、もし標本抽出枠が無い場合は母集団の要素を自力でリストアップする。現代ではコンピューターで電話番号の標本抽出枠を生成するRDD法(Random Digit Dialing)など様々な方法が実用化されている。
標本抽出枠から要素を無作為に抽出するには、まず標本抽出枠の全ての要素に通し番号を振り、そこから抽出する番号を乱数で決める必要がある。乱数の生成方法は、昔は乱数表や乱数さいなどが使われた時代もあったが、現代では普通コンピューターの擬似乱数が使われる。
単純無作為抽出法
[編集]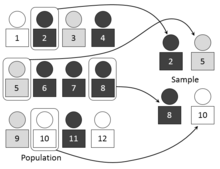
単純無作為抽出とは、母集団の全ての要素を対象として無作為抽出する方法である。無作為抽出の最も基本的な方法で、もっとも単純な方法である。
単純無作為抽出法以外では、「標本抽出枠に何らかの規則性がないか」とか「全校生徒の男子と女子の比率」などの様々な情報が必要になるのとは違い、単純無作為抽出法は「抽出枠」の情報さえあれば行うことが出来、抽出枠の大きさが小さい場合はこの手法を使うのが最も楽である。しかし、抽出枠が大きい場合は非常に手間と時間がかかるので、「層化」や「多段抽出」を行った方が楽である。
系統抽出とは違い、隣り合った要素同士が選ばれたり、3個以上連続した要素が選ばれる可能性がある。住民の意識調査などでは、同じ世帯の人は同じ意見を持つ可能性が高いので、同じ世帯から複数の人が抽出される可能性が有ることは、デメリットになる。ただし、抽出枠が非常に大きい場合は、隣り合った要素同士が選ばれる可能性はほとんどないので、あまり気にされない。
系統抽出法
[編集]
抽出枠の「先頭から m 番目」の要素を開始点として、そこから「n つ飛ばし」に、要素をそれぞれサンプリングする方法(m, n はそれぞれ任意の数)。要素を等間隔に抽出するので等間隔抽出法とも言う。
まず、抽出単位の総数を抽出数で割って抽出間隔を求める。例えば12人の生徒の中から4人の掃除当番を選ぶ場合、12を4で割った答えは3であるから、3人ごとに抽出を行えばよい。その後、先頭の3人の中から開始点を無作為に決める。この時に選んだ乱数を「スタート乱数」と言う。スタート乱数を作為的に選んだ場合は無作為抽出にならないが、スタート乱数を無作為に選んだ場合、全ての要素が同じ確率で選ばれる無作為抽出となる。
抽出単位の総数を抽出数で割った際に余りが出る場合、例えば13人の生徒の中から4人の掃除当番を選ぶ場合、上記の方法でサンプリングを行い、3人ごとに抽出を行っていって4人が選出された時点でサンプリングを終了したとすると、出席番号13の奴が抽出枠から外れることになって不公平である。この場合、13人目以降もいるというテイで、さらにもう1回同様のサンプリングを続けて試行することで、全ての生徒が同じ確率でサンプリングされる無作為抽出となる。もう1回サンプリングを試行した結果、もし出席番号13の奴が5人目の掃除当番としてサンプリングされてしまった場合、5人の中からさらに抽選を行って4名を抽出するとよい。(なお、現実にはそこまで確率的に厳密にすることはあまりなく、スタート乱数は作為的に決められ、割った余りの人を抽出枠に含めるか含めないかも作為的に決められることが多い)
隣り合った要素がサンプリングされることが無いのが特徴。また、「n 番目」を系統的(システマティック)に選出するだけなので、乱数発生器が使えない場合、つまりコンピュータが使えない状況でも人力で行うことが出来る。例えば1200人の全校生徒の中から400人の掃除当番を選ぶ際、系統抽出法を使うとするなら、1から3まで書かれたルーレットを自作して1回回してスタート乱数を決めるだけで、後は掃除当番の人がシステマティックに選出される。無作為性は低くなるが簡易な乱数生成器(現在時刻、脳内でルーレットを回すなど)を使ってスタート乱数を決めた場合、生徒の数に関わらず一瞬で掃除当番の人が決まるのも大きなメリットである。もし単純無作為抽出法を使うとするなら、1から1200まで書かれたルーレットを自作して400回回す必要があり、現実的ではない。
「3の倍数の時にアホが並んでいる名簿」から3つ飛ばしにサンプリングする場合など、標本抽出枠に何らかの規則性が有る場合、無作為抽出にならない欠点がある。
層化抽出法
[編集]母集団をあらかじめいくつかのグループ(層)に分け、それぞれのグループで単純無作為抽出を行う「層化」と呼ばれる手法を用いる。
例えば世論調査では、都道府県別・自治体別などに分けてサンプリングする層化抽出法が行われている。母集団の要素数が約1億2000万のデータを「抽出枠」として使って単純無作為抽出するよりも、層化した方が楽だし、都道府県別の世論も見られるメリットがある。ただし、携帯電話のRDD方式の世論調査だと市外局番が使えない[注 1]ので、コンピュータで制作した数億の抽出枠から機械の力で単純無作為抽出せざるをえない[注 2]。このように、「抽出枠」の情報に加えて「層化」を行うための情報がないと母集団を層化できないデメリットがある。
各層で分布が大きく異なる場合に効果を発揮する。例えば、東京都(人口が約1300万人)から鳥取県(人口が約60万人、東京23区全体どころか練馬区や世田谷区よりも人口が少ない)まで、人口比が著しく異なる都道府県からなる日本列島からまんべんなく人間を無作為抽出する場合に、単純無作為抽出だと人口が少なくてサンプリングされない地方民が出る場合があるが、都道府県ごとに層化すると、そういうことがない。都道府県別に分けてサンプリングしても、全ての日本国民でサンプリングされる確率が同じなら、無作為抽出である。
詳しく言うと、比例配分法(比例割当法)と最適配分法(最適割当法)がある。
比例配分法
[編集]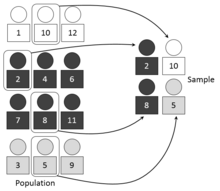
層化抽出法の一種で、各層の大きさに比例させて標本数を配分する。
例えば学校では、全校生徒から単純無作為抽出するよりも、男子と女子の比率に合わせてサンプルを揃えた方が都合が良い場合、「男子」と「女子」と言う層の大きさに合わせて標本数を決める。男子と女子で別々にサンプリングしても、男子と女子でサンプリングされる確率が同じならば、無作為抽出である。
あらかじめ全数調査するなどして、各層の比率が分かっていないと行えないという欠点がある。
最適配分法
[編集]層化抽出法の一種で、各層の大きさに合わせて最適な標本数を配分する。「ネイマン・ピアソン理論」(「推計統計学」の基本となる理論)の確立者の一人でもあるイェジ・ネイマンが考え出したので「ネイマン配分法」ともいう。
例えば、企業の生産高を見るとき、一定規模以上の大企業は全数調査し、一定規模以下の中小企業は単純無作為抽出によるサンプリング調査をして全体を推定する、と言う形で、各層に最適なサンプリング数を配分する。
クラスター抽出法
[編集]
母集団をいくつかのクラスターに分け、その中からいくつかのクラスターを無作為抽出し、それを全数調査する。
例えば、市内の高校生を高校ごとに分け、その中から3つの高校を無作為抽出し、その高校に通う高校生を全数調査する。
この例では、市内の全ての高校生において選ばれる可能性が同じであるため、無作為抽出である。高校生の代表としてワルばかりいる高校の生徒を大量にサンプリングしてしまう可能性もあるなど、単純無作為抽出法などよりも代表性が低くなってしまうという欠点がある。しかし市内の全ての高校に行って調査しなくていいのは楽であり、利点である。
多段抽出法
[編集]母集団をいくつかのグループに分け、そこからランダムにグループを抽出する。抽出されたグループの中からさらにランダムにグループを抽出…と言う作業を何度か繰り返し、何段階かに分けてサンプルを抽出する方法。
例えば、全国の高校生から500人をサンプリングする場合、全国の都道府県の中から10の都道府県を無作為抽出する。抽出された都道府県ごとに10の高校を無作為抽出する。抽出された高校ごとに5人を無作為抽出する、と言う形である。つまり、単純無作為方式を階層化して実行する。全国の全ての高校生において選ばれる可能性が同じであるため、無作為抽出である。クラスター抽出法と同じく、単純無作為抽出法などよりも代表性が低くなってしまうという欠点がある。
標本調査における無作為抽出と有意抽出の比較
[編集]標本調査における標本抽出の方法としては、「無作為抽出」の他に「有意抽出」がある。母集団を代表する標本を無作為に抽出したものを「無作為抽出」と呼ぶのに対して、母集団を代表する標本を有意に抽出したものを「有意抽出」と呼ぶ。
標本調査は全数調査とのズレ(誤差)が発生することが必ず避けられないが、無作為抽出法を用いた標本調査において発生する誤差(標本誤差)の範囲が確率論に基づいて統計学的に計算できるのに対し、有意抽出法を用いた標本調査において発生する誤差の範囲は確率論的に計算することが出来ず、不明となる。
インターネットのモニターによる市場調査(モニター調査)を例にすると、インターネットによる自発記入のアンケートを用いて標本を集めるので、非常に手軽にできるというメリットがある反面、1)インターネットを利用できる環境にある人、2)アンケートに関心を示した人、のようにサンプル自体に偏りが生じる。サンプル自体に偏りがあるため、このモニター調査の結果が全数調査の結果(真の値)とどの程度ずれているかの範囲は、統計学的に算出することが出来ず、客観的に信頼性が置けるデータがゲットできない、と言うのがデメリットである。
このため、例えば世論調査など客観的な信頼性が重視される統計調査では、いくら手軽にできても有意抽出法は使われず、面倒な手順を踏んでも必ず無作為抽出法が使われる。
関連項目
[編集]脚注
[編集]注
[編集]出典
[編集]- ^ JIS Z 8101-1 : 2015, 1.6 無作為標本.
参考文献
[編集]- 日本数学会『数学辞典』岩波書店、2007年。ISBN 9784000803090。
- JIS Z 8101-1:2015 統計 − 用語と記号 − 第1部:確率及び一般統計用語, 日本規格協会, (2015)
