コンテンツにスキップ

水晶振動子マイクロバランス

出典: フリー百科事典『ウィキペディア（Wikipedia）』
QCM用に広く流通している水晶の振動子。金を蒸着して電極としている（左: オモテ面電極、右: 背面電極）。

水晶振動子マイクロバランス（すいしょうしんどうしマイクロバランス、quartz crystal microbalance: QCM 、または quartz microbalance: QMB、quartz crystal nanobalance: QCN）は、水晶振動子の周波数変化を測定することで、単位面積当たりの質量変動を測定する装置である。振動子表面での酸化物の増減や薄膜の堆積により質量が微小に増減すると、振動子の周波数が変化する。QCMは真空下、気相中（「ガスセンサー」としてKingが初の使用を報告[1]）、最近では液体環境でも使用される。真空中の薄膜堆積システムでは堆積速度のモニタリングに使用できる。液体中では、分子（特にタンパク質）と、その分子を認識できる官能基を付加した表面との間に起こる親和性の強さを効果的に測定できる。ウイルスや高分子などの大きな分子体の研究にも使用される。QCMは生体分子間の相互作用研究にも使用されている。周波数は高精度で測定できるため、1 μg/cm2未満の質量密度も容易に測定できる。周波数そのものの測定に加え、振動子の周波数変化の幅に相当する散逸率を測定して解析に用いることもある。散逸率は、振動のQ値の逆数であり、Q-1 = ω/frである。これは系の振動減衰を定量化するものであり、試料の粘弾性特性と関連する。

概要

[編集]

適切な形状の水晶振動子は交流の電流を印加すると厚みすべり振動（Thickness-shear-mode resonator）により、一定の周波数で振動する[2]。この周波数は水晶の厚みに依存し、薄いほど高周波数で発振する。1950年代に水晶振動子の電極上の物質の質量に応じてその周波数とQ値が変化する事象が報告された。水晶表面への物質堆積により厚みが僅かに増大した結果、振動数が初期値から減少するためである。いくつかの単純化した仮定を用いれば、この振動数の変化を定量化し、Sauerbrey方程式を用いて質量変化と正確に相関させることができる[3]。この水晶振動子の周波数変化を検出することにより、電極上での物質の質量変化を計測する方法を水晶振動子マイクロバランス法（QCM法）と呼ぶ[2][4][5]。

Sauerbreyの方程式

- 基本周波数 (Hz)
- 周波数の変移 (Hz)
- 質量の変移 (g)
- 圧電効率 能動面積 (電極間の面積 cm2)
- 水晶の密度 ( = 2.648 g/cm3)
- AT-カット水晶の剛性率 ( = 2.947×1011 g·cm-1·s-2)

Sauerbreyの方程式を見ると、右項の分子に水晶振動子の基本周波数f0が入っており、これは水晶振動子の基本周波数を高くすればするほど周波数の2乗に比例して検出される振動数変化の値が大きくなることで質量検出感度が向上することを意味する。27 MHzの基本振動数を持つ水晶振動子の場合、1 Hzの振動数減少が0.62 ng/cm2のセンサー表面上の質量増加を示すことが理論的にも実験的にも確認されている[2]。

以前は水晶板の振動が液相のように粘性の高い環境では強く減衰されてしまうために発振できないことや、水晶振動子の構造が金属薄膜で絶縁体である水晶を挟んだ一種のコンデンサーなので水中のような導電性の雰囲気中では両電極が通電してしまうことなどの問題点があったため、気相中の分子の測定に限られていたが、近年では液相中の分子の測定にも使用される[2]。

薄膜の特性を測定するための他の関連技術としては、エリプソメトリー、表面プラズモン共鳴（SPR）分光法、マルチパラメトリック表面プラズモン共鳴、二重偏光干渉法が挙げられる。

特徴

[編集]
  • センサー表面へのナノグラムレベルの吸着量を定量化可能[2]。
  • タンパク質などの生体分子でもラベル化することなく、in vivoに近いかたちで相互作用を検出できる[2]。
  • 吸着反応をリアルタイムに測定できる[2]。

用途

[編集]

もっとも古典的なQCMの応用例の一つが微量重量測定（重量QCM）である[6][7][8][9][10][11]。常温常圧下で簡便な装置を用いて、微小量（単原子膜層レベル）の重量変化を用意に測定できるため、気相中の化学物質の検出や薄膜蒸着時の膜厚測定などに古くから利用されてきた。薄膜が十分薄い場合、共振周波数は振動子の総厚に反比例するとみなせる。しかし膜厚が大きくなると、粘弾性効果を無視できなくなり、その大きな減衰効果の考慮が必要となる[12]。特に液体中では粘弾性効果の共振特性への強い寄与が問題となる。1980年代後半には、適切な対策を講じることで、QCMは液体中でも動作可能であることが見出された[13][14]。現在では、粘度や粘弾性特性の測定もQCMの重要な応用例となっている（非重量QCM）[15]。

表面弾性波センサにおける位置づけ

[編集]

QCMは、表面における音響波に基づく、より広い分類のセンシング装置の一つである。同様の動作原理を共有する装置には、せん断水平表面弾性波（SH-SAW）装置[16][17]、弾性表面波装置[18] 、ねじり共振器[19][20]などがある。表面弾性波ベースの装置は、結晶表面における音響波の反射率が、隣接する媒質のインピーダンス（応力対速度比）に依存するという特性を利用している。これらの表面音響波に基づくセンシングの文脈では、QCMは「バルク音響波共振器(BAW-resonator)」または「厚み-せん断共振器」とも呼ばれる。無負荷のBAW共振器の変位パターンは、結晶表面に反ノードを持つ定在せん断波であり、解析の容易性にすぐれている。

装置

[編集]

共振体

[編集]

QCMが開発された当初は、天然の水晶を採取・選別した後に実験室でカットして使用していた。現在では、種水晶から成長させた人工水晶が用いられている。成長した結晶はカットされ、1～30MHzの範囲の厚みせん断共振をサポートする髪の毛ほどの薄さの平板へと研磨される。実用場面では"AT"または"SC"配向カットがおもに利用されている[21]。研究レベルでは、水晶の代替材料としてランガサイト（La3Ga5SiO14、「LGS」）やガリウムオルトホスフェート（GaPO4）が研究されており、高温で動作可能といった特性が報告されている[22][23] 。これらの代替材料を用いて作成したデバイスは水晶で構成されていないが、慣例的に「QCM」と呼ばれることがある。

圧電効果の影響

[編集]

QCMは、両面に電極が蒸着された薄い圧電板で構成されている。したがって、電極を横切る交流電圧を印可することで圧電効果によりせん断変形を誘発する。同様に、せん断変形は電極を横切る交流電圧を誘発する。この圧電効果は、圧電剛性を介して共振周波数にわずかな影響を与えうる。本効果をセンシングへと応用した研究例もある[24]が、通常の用途では忌避される現象である。圧電効果の影響を避けるには、電気的・誘電的境界条件を十分に制御することが不可欠である。そのための方法の一つが、前面電極（試料と接触する電極）を接地である。同じ理由で「πネットワーク」が採用されることもある[25]。πネットワークは、2つの電極をほぼ短絡させる抵抗の配列である。これにより、デバイスは電気的摂動の影響を受けにくくなる。

液体と気体中のせん断波の減衰

[編集]

ほとんどの音響波センサは圧縮波（縦波）ではなくせん断波（横波）を利用する。圧縮波は共振体と接するバルク（液体や気体）に対して放射され、測定セル内壁で反射して共振体へと影響を与えうるのに対し、せん断波は液体や気体の環境では急速に減衰するため、このような反射を回避することが出来る[26][27]。例えば、水中での5 MHzのせん断波の浸透範囲はわずか250 nmである。この有限の浸透深さにより、QCMの検知範囲は表面特異的となる。さらに、液体や気体のせん断音響インピーダンスはかなり小さいため、共振体自体の振動を減衰させる効果は小さい。このように周辺環境との結合が弱いために、音響共振器は例外的に高いQ値を得ることが出来る。

動作モード

[編集]

QCMを駆動する経済的な方法は、発振回路を利用することである[28][29] 。発振回路は、発振器がクロックとして機能する時間および周波数制御アプリケーションでも広く採用されている。その他の動作モードには、インピーダンス解析[30]、QCM-I、およびリングダウン[31][32]QCM-Dがある。インピーダンス解析では、ネットワーク・アナライザを使用して、駆動周波数の関数としての電気コンダクタンスを決定する。コンダクタンス曲線に共振曲線をフィットさせることで、共振の周波数と帯域幅がフィッティングパラメータとして得られる。リングダウンでは、励起電圧を急激にオフにした後の電極間電圧を測定する。共振器は減衰する正弦波を発し、共振パラメータは発振周期と減衰率から抽出される。

インピーダンス解析にもとづく電気伝導曲線。測定の中心となるパラメータは、共振周波数fresと帯域幅wである。
リングダウンはtime-domain測定で同等の情報を与える。散逸率DはQ-1に等しい。

エネルギーの閉じ込め

[編集]

水晶の縁に接触する水晶ホルダーによる振動エネルギーの散逸（振動の減衰）を避けるため、振動は水晶板小片の中心に閉じ込める必要がある(エネルギー・トラップ)。

高周波数（10MHz以上）の水晶の場合、水晶の前面と背面の電極は通常鍵穴様の形状となっており、それによって共振器は縁よりも中央の方が厚くなる。電極の質量により、変位磁場が水晶ディスクの中心に閉じ込められる[33]。振動周波数が5、6 MHz付近のQCM水晶は通常、平凸形状をしている。したがって、どちらの場合も、厚み-せん断振動の振幅は円盤の中心で最大となる。このことは、質量感度も中心でピークに達し、この感度は縁に向かって滑らかにゼロに減少することを意味する（高周波水晶の場合、振幅は小さい方の電極の外周のやや外側で消失する[34]）。したがって、質量感度は水晶表面全体で非常に不均一であり、この不均一性は金属電極の質量分布（または非平面共振器の場合は水晶の厚さ自体）の関数となる。

表面弾性波は本来平面波であるが、エネルギーの閉じ込めによってわずかに歪むことになる。この平面的な厚み-せん断モードからの逸脱によって、変位パターンは屈曲寄与を伴うことになる。結晶を真空中で使用しない場合、この屈曲波は隣接する媒質に圧縮波を放出する。そして結晶と測定容器の壁（または液面）の間の液体中に定在圧縮波が形成され、この波が水晶振動子の周波数と減衰の両方を変化させる効果を及ぼす。

倍音

[編集]

平面共振器は、一般に、結晶面に平行な節面の数で示される数の倍音で動作させることができる。奇数倍音のみを電気的に励起することができるのは、これらの倍音のみが2つの結晶表面で逆符号の電荷を誘起するからである。倍音は、共振器の平面に垂直な節面を持つ非調和サイドバンド（スプリアスモード）と区別される。理論と実験が最もよく一致するのは、光学的に研磨された平面結晶で、n=5からn=13の間の倍音次数である。低次倍音ではエネルギー捕捉が不十分であり、高次倍音では非調和的なサイドバンドが主共振を妨害する。

振幅

[編集]

横方向の変位の振幅がナノメートルを超えることはほとんどない。より具体的には、変位は以下の式で記述される。

ここで、u0は横変位の振幅、nは倍音次数、dは圧電ひずみ係数、Qは「Q値」、Uelは電気駆動の振幅である。圧電歪み係数は、ATカット水晶の場合、d=3.1-10-12 m/Vとして与えられる。振幅が小さいため、応力とひずみは通常互いに比例する。つまりQCMは線形音響の範囲で動作する。

温度と応力の影響

[編集]

音響共振器の共振周波数は、温度、圧力、曲げ応力の影響を受ける。したがって、QCMの動作には温度と応力の慎重な制御が不可欠である。特殊な水晶カットを採用することで、この温度と周波数のカップリングを最小限に抑えることが可能である。広く使われている水晶の温度補償カットはATカットである。

ATカット水晶は、Y軸を回転させた特異なカットで、発振中に水晶の上半分と下半分が反対方向に動く（厚みせん断振動）[35][36] 。ATカット結晶は極端な温度勾配によって生じる内部応力によって容易に破壊されるため、高温や低温における使用には限界がある。さらにこれらの内部応力点は、結晶に望ましくない周波数シフトを生じさせ、精度を低下させる。温度と周波数の関係は3次曲線である。この3次関係は室温付近で変曲点を持つ。よって、ATカット水晶振動子は室温または室温付近で動作させる時に最も効果的である。室温を超えるうる用途では水冷が有効な場合が多い。ATカットは製造が容易で安価であることから、商業的にひろく用いられている。

高温動作時の温度勾配による周波数変化を最小限に抑えるためには、ストレス補償（SC）カット水晶振動子が利用可能である[37]。SCカットはATカットと比較して変曲点が高温（約92 °C）であり、かつより滑らかな3次曲線関係を持つことから、屈曲点からの温度偏差に対しても影響を受けにくい特性がある。ただし、製造プロセスの難しさから高価であり、商業的には広く用いられていない。

電気化学QCM

[編集]

詳しくはen:Electrochemical quartz crystal microbalanceを参照。 QCMは他の表面分析装置と組み合わせることができる。特に電気化学QCM（EQCM）の進展は著しい[38][39][40]。EQCMを用いると、電極を通過した全電荷に対する、電気化学反応中に電極表面に堆積した質量の比を求めることができる。この比は電流効率と呼ばれる。

散逸過程の定量化

[編集]

QCM-IやQCM-Dのような高度なQCMでは、共振周波数frと帯域幅wの両方を解析することができる。後者は振動からエネルギーを奪うプロセスを定量化する。これには、ホルダーによる減衰や、電極や結晶内部のオーミック損失が含まれる。帯域幅を定量化するために、w以外のパラメータを用いている研究例もある。Q値（品質係数）はQ = fr/wで与えられる。散逸係数Dは、Q値の逆数である（D = Q-1 = w/fr）。半値幅Γは帯域幅の半分の値（Γ = w/2）である。Γは、結晶の運動を支配する方程式の複雑な定式化する際に用いられる。複素共振周波数はfr* = fr + iΓと定義される。複素数表記を使うことで、周波数シフトΔfと帯域幅ΔΓを同じ方程式内で扱うことが可能となる。

共振器の運動抵抗 R1 も、散逸の尺度として使用される。R1は、高度な発振回路に基づく機器の出力パラメータである。後述のBvD回路モデルに基づけばR1は理論的には帯域幅wに比例するはずであるが、通常、R1はwに厳密には比例しない。またR1 は周波数ではなく電気量であるため、帯域幅よりも校正問題の影響を大きく受ける[41]。

等価回路

[編集]

音響共振器は一般に等価電気回路を用いてモデル化される[42]。等価回路は、連続体力学に基づく記述[43]や音響反射率による記述[44]と代数的に等価である。これらの記法は単なる比喩表現ではなく、負荷変調に応じた共振パラメータの変化を予測するための道具として実用されている。

等価回路は電気-機械結合系的なアナロジーに基づいている。抵抗のネットワークを流れる電流が抵抗の配置と印加電圧から予測できるのと同じように、機械的要素のネットワークの変位はネットワークのトポロジーと印加される力から予測できる。電気-機械結合系的なアナロジーは、力を電圧に、速度を電流に変換する。力と速度の比は「機械インピーダンス」と呼ばれる（ここでいう速度とは、音速ではなく変位の時間微分を意味する）。また、電気音響学的な類似性もあり、そこでは（力ではなく）応力が電圧にマッピングされる。音響学では、力は面積に正規化される。なお、応力と速度の比を「音響インピーダンス」と呼ぶのは避けるべきである（機械的インピーダンスのアナロジー）。この用語は、材料特性Zac = ρc（ρは密度、cは音速）で既に使用されているからである。結晶表面における応力と音速の比は、負荷インピーダンスZLと呼ばれる。同義語は「表面インピーダンス」と「音響負荷」である[29]。負荷インピーダンスは一般に、材料定数Zac = ρc = (Gρ)1/2には等しくない。ZLとZacの値が同じになるのは、伝播する平面波の場合だけである。

電気-機械結合系的なアナロジーでは、抵抗、インダクタンス、キャパシタンスに相当する機械的なものとして、dダンパー（抗力係数ξpで定量化）、点質量（質量mpで定量化）、バネ（バネ定数κpで定量化）がある。ダンパーの場合、インピーダンスの定義はZm=F / (du/dt)=ξm (Fは力、(du/dt)は速度)である。振動運動をする点質量u(t) = u0 exp(iωt)の場合、Zm = iωmpとなる。バネはZm =κp/(iω)に従う。圧電カップリングは変圧器として記述される。これはパラメータφによって特徴付けられる。通常の変圧器ではφは無次元（巻数比）だが、電気-機械結合系の場合は電荷/長さの次元を持つ。トランスは、機械的インピーダンスZmが電気的インピーダンスZelとして電気ポートを横切って現れるという意味で、インピーダンス変換器として機能する。 ZelはZel = φ2 Zmで与えられる。平面圧電結晶の場合、φはφ = Ae/dqの値をとり、Aは有効面積、eは圧電応力係数[30]（ATカット水晶の場合、e = 9.65·10-2 C/m2）、dqは振動子の厚さである。トランスは明示的に記述されないことが多い。むしろ、機械的要素は電気的要素 (コンデンサがバネに置き換わるなど) として直接記述される。

電気-機械アナロジーの適用には落とし穴があり、それはネットワークの描き方に関係している。バネがダンパーを引っ張る場合、通常は2つの素子を直列に描く。しかし、電気機械のアナロジーを適用する場合、2つの要素は並列に配置されなければならない。並列の2つの電気素子では、電流は加算される。ダンパーの後ろにスプリングを配置すると、速度（=電流）が加算されるため、この組み合わせは並列ネットワークで表現しなければならない。

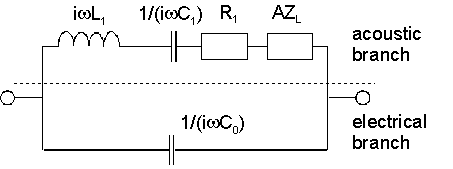
Butterworth-Van Dyke（BvD）等価回路. C0 は電極間の電気（並列）容量. L1は運動インダクタンス（質量に比例）. C1C1は運動容量（剛性に反比例）. R1は運動抵抗（散逸損失を定量化）. Aは水晶の有効面積. ZLは負荷インピーダンス.

右の図はButterworth-Van Dyke（BvD）等価回路である。水晶の音響特性は、運動インダクタンスL1、運動キャパシタンスC1、運動抵抗R1で表される。ZLは負荷インピーダンスである。負荷インピーダンスZLは、一度の測定で求めることは出来なず、負荷がかかった状態と負荷がかかっていない状態との比較から算出される。この回路は「4要素ネットワーク（four element network）」とも呼ばれる。L1, C1, R1の値は（ZLが明示的に含まれていない限り）負荷の存在下で変化する。

小負荷近似

[編集]

BvD回路は共振パラメータを予測する。周波数シフトが周波数そのものよりもはるかに小さい限り、以下の単純な関係が成り立つことを示すことができる（小負荷近似）。[8]

ffは基本周波数である。 Zqは材料の音響インピーダンスである（ATカット石英の場合、Zq = 8.8-106 kg m-2 s-1）。

小荷重近似はQCMデータの解釈において最も普通の手法である。これは任意のサンプルに対して成立し、平均的な意味で適用できる[nb 1][45]。 試料が培養細胞や粒子や泡の集合体、液滴などの複雑な物質であると仮定した場合でも、仮に結晶表面における試料の平均応力対速度比（負荷インピーダンス、ZL）を何らかの方法で計算することが出来るなら、QCM実験の定量的分析が可能となる[46]。そうでない場合は、定性的な解釈に留まらざるを得ない。

周波数シフトが大きい、あるいは試料の粘弾性特性を導き出すためにΔfとΔ(w/2)の倍音依存性を詳細に分析する際に、小荷重近似の適用限界が問題となる。より一般的な関係は以下の通りである。

この方程式はΔf*における陰関数であり、数値的に解かなければならない。 小荷重近似とは別の近似解も存在する。小荷重近似は摂動論に基づく1次解である[47]。

負荷インピーダンスの定義は、応力と速度が比例し、その比が速度に依存しないことを暗黙の前提としている。この仮定は、線形音響学の法則が成立する場合（水晶振動子が液体中や空気中で動作する場合）には用いることができる。しかし、水晶振動子が粗い表面と接触している場合、応力は有限個の小さな荷重を支えるアスペリティを横切って伝達されるため、応力はしばしばひずみ（および速度）の非線形関数となる。接触点の応力は高くなり、すべり・部分すべり・降伏などの現象が生じる。これらは非線形音響学で扱われる範疇の問題である。小荷重を仮定できる場合、この問題を取り扱い可能な一般的な方程式がある。 応力σ(t)が時間的に周期的かつ結晶振動と同期している場合、次の式が成立する。

角括弧は時間平均を表し、σ(t)は外部表面によって及ぼされる（小さな）応力である。 関数σ(t)は調和的であっても非調和的であっても良い。駆動電圧に対する共振パラメータの依存性を確認することで、非線形挙動を示すか否かを常にテストすることが可能である。線形音響学が成り立つなら、各パラメータの駆動電圧依存性は存在しないはずである。ただし、水晶振動子自体も固有の駆動電圧依存性がを有しており、これを振動子と試料の間の非線形相互作用と混同しないように注意する必要がある。

粘弾性モデル

[編集]

前提条件

[編集]

後述するように、多くの典型的な実験構成について、周波数と帯域幅のシフトとサンプル特性とを関連付ける理論式が知られている[48][49][50][51]。それらの方程式の多くに共通する暗黙の仮定は以下の通りである：

  • 共振器とすべてのカバー層は横方向に均質であり、無限である。
  • 結晶の歪みは、波動ベクトルが表面法線に垂直な横波平面波によって与えられる（厚み-せん断モード）。変位パターンには圧縮波[25][26]も曲げモード[52]も寄与しない。共振器の平面には結節線がない。
  • すべての応力はひずみに比例する。線形粘弾性が成り立つ[53]。
  • 圧電剛性は無視できる。

半無限粘弾性媒体

[編集]

半無限媒質の場合、以下が成立する[54][55][56]。

η’とη’’はそれぞれ粘度の実部と虚部である。Zac = ρc =(G ρ)1/2 は媒質の音響インピーダンスであり、ρは密度、cは音速、G= i ωηはせん断弾性率である。 ニュートン液体（η’ = const, η’’ = 0）では、ΔfとΔ(w/2)は等しく反対である。 これらは倍音次数n1/2の平方根としてスケールする。粘弾性液体（η’=η(ω)、η’’≠ 0）の場合、複素粘性率は次のように求めることができる。

重要なことは、QCMは結晶表面にごく近い領域のみが観測範囲となるということである。したがって、表面粗さ、ナノバブル、スリップ、圧縮波が粘度測定の妨げになることがある。また、高周波数（MHzなど）で測定された粘度は、低周波の粘度と異なることがある。この点で、ねじり共振器[20]（周波数100 kHz前後）は、厚みせん断共振器よりもより実用条件に近い。

慣性負荷 (Sauerbrey方程式)

[編集]

詳しくはen:Sauerbrey equationを参照。 結晶に強く結合された薄い試料（薄膜など）によって誘起される周波数シフトはSauerbrey方程式で記述される。ここでu0は振動の振幅、mFは単位面積あたりの（平均）質量である。この結果を小荷重近似に入れると以下が成立する。

膜の密度がわかっていれば、単位面積あたりの質量mFから厚さdFに変換できる。このようにして導き出された厚さは、周波数シフトにSauerbrey方程式を適用して導き出されたことを示すためにSauerbrey厚とも呼ばれる。Sauerbrey方程式が成り立つ場合、帯域幅のシフトはゼロである。したがって、帯域幅をチェックすることは、Sauerbrey方程式の適用可能性をチェックすることになる。

Sauerbrey方程式は1959年にen:Günter Sauerbreyによって初めて導出されたもので，圧電結晶の振動周波数の変化とその上に堆積した質量との相関を示す．彼は同時に、水晶振動子を発振回路の周波数決定成分として使用することで、共振周波数とその変化を測定する方法を開発した。彼の方法は、周波数を質量に変換するための水晶振動子マイクロバランス実験における主要なツールとして現在も使用されている。

膜は厚みの延長として扱われるため、Sauerbreyの式は、(a) 堆積した質量が水晶と同じ音響特性を持ち、(b) 周波数の変化が小さい（Δf / f < 0.05）系にのみ適用される。

周波数の変化が5%より大きい場合、つまりΔf / f > 0.05の場合、Z-match法を用いて質量の変化を決定しなければならない[12][56]。Z-match法の公式は以下のとおりである。

kF は膜内部の波動ベクトルであり、dF はその厚さである。kF = 2·π·f /cF = 2·π·f·ρF / ZF と dF = mF / ρF を代入することで以下が得られる。

粘弾性膜

[編集]

粘弾性膜の場合、周波数シフトは次のようになる。

ここで、ZF は膜の音響インピーダンスである (ZF = ρFcF = (ρFGf)1/2)= (ρF/Jf)1/2), kF は波動ベクトルであり、dF は膜厚である。Jf は膜の粘弾性コンプライアンス、 ρFは密度である。

接線の極 (kF dF = π/2) は膜共振を定義する[57][58]。膜共鳴ではdF = λ/4となる。膜共鳴の付近ではしばしば実験と理論の一致が悪くなる。一般的に、QCMがうまく機能するのは、音波長の4分の1よりもはるかに小さい膜厚（膜の柔らかさや倍音次数にもよるが、数マイクロメートルに相当する）の場合だけである。

QCMで決定される膜の特性は、音響インピーダンスZF = ρFcFと単位面積あたりの質量mF = dF/ρFの2つのパラメータによって完全に規定されていることに注意すべきである。波数kF = ω/cFは、ZF と mFから代数的に独立していない。膜密度が独立して分かっていない限り、QCMは単位面積あたりの質量しか測定できず、幾何学的な厚さそのものを測定することはできない。

液体中の粘弾性膜

[編集]

液体に浸された膜の場合、周波数シフトは以下で表される[59][60]。

添え字FとLiqはそれぞれ膜と液体を表す。ここで、標準状態は液体に浸された（膜で覆われていない）状態の結晶である。薄膜の場合、上の式をdFの一次式までテイラー展開すると、次のようになる。

括弧内の項を除けば、この方程式はSauerbrey方程式と等価である。括弧内の項は粘弾性補正であり、液体では柔らかい層は硬い層よりも小さなSauerbrey厚になるという実験事実を扱うことができる。

粘弾性定数の導出

[編集]

周波数シフトは材料の音響インピーダンスに依存する。周波数シフトは材料の音響インピーダンスに依存し、後者は材料の粘弾性特性に依存する。したがって、原理的には複素せん断弾性率（あるいは複素粘性率）を導出することができる。しかし、いくつかの注意点がある：

  • 粘弾性パラメータ自体は通常、周波数（したがって倍音次数）に依存する。
  • 慣性の影響と粘弾性の影響を切り離すのは難しいことが多い。膜厚が独立してわからない限り、独自のフィッティング結果を得ることは難しい。
  • 電極効果は重要である。
  • 空気中の薄膜の場合、膜が非常に軟らかくない限り、小荷重近似は摂動理論からの対応する結果で置き換える必要がある。

液体中の薄膜については、薄膜の弾性コンプライアンスJF'をΔ(w/2)とΔfの比に関連付ける近似的な解析結果がある。せん断コンプライアンスは、せん断弾性率の逆数Gである。薄膜限界では、Δ(w/2)と-Δfの比は膜厚に依存しない。これは膜の本質的な特性である[61]。

気相中の薄膜についても、類似の解析結果がある[62]。

ここでJは粘性せん断コンプライアンスである。

Sauerbrey厚の解釈

[編集]

液中のQCM測定から得られる周波数シフトを正しく解釈することは難しい。Sauerbrey厚は、異なる実験を比較するのに役立つことは確かであるが、幾何学的厚さと素朴に同一視してはならない。考慮すべき点は以下の通りである:

a) QCMは常に面質量密度を測定しており、決して幾何学的厚さを測定しているわけではない。面的質量密度から厚さへの変換には、通常、物理的密度を独立した入力として必要とする。

b) QCMデータから粘弾性補正係数を推測することは困難である。しかし、補正係数が単一から大きく異なる場合、それは帯域幅Δ(w/2)に影響し、また倍音次数に依存することが予想される。逆に、そのような影響がない場合（(Δ(w/2) « Δf, Sauerbrey厚がすべての倍音次数において等しいと見なせる場合)、(1-ZLiq2/ZF2)≈1と仮定することができる。

c) 複雑なサンプルはしばしば横方向に不均一である。

d) 複雑な試料は、しばしば複雑な界面を持つ。 柔らかな（fluffy）界面はしばしば粘弾性補正を引き起こし、その結果、ゼロでないΔ(w/2)や倍音に依存するSauerbrey質量をもたらす。このような効果がない場合、膜の外側の界面は固い（sharp）と結論づけることができる。

e) (b)で議論した粘弾性補正が重要でない場合、これは決して膜が溶媒によって膨潤していないことを意味しない。膨潤した膜が周囲の液体よりもはるかに硬いことを意味するだけである。よって、湿潤試料だけで得られたQCMデータだけでは膨潤の程度を推測することはできない。 膨潤量は、湿潤時と乾燥時の厚さの比較から推測することができる。表面プラズモン共鳴（SPR）分光法やエリプソメトリーなどで測定した光学的厚みと音響的厚み（Sauerbrey法）を比較することでも、膨潤の程度を知ることができる。膜に含まれる溶媒は通常音響的な厚みに寄与するが、光学的な厚みには寄与しない（溶媒分子の分極率は、それが膜内部にあるときには変化しないため）。乾燥質量と湿潤質量の違いはQCM-DとMP-SPRを用いて、例えばナノセルロースへのタンパク質吸着[63][64] やその他のソフトマテリアル[65]の系で示される。

点接触

[編集]

粘弾性特性に関する方程式は平面積層系を想定している。周波数シフトは、結晶が小さな、荷重を受けるアスペリティを横切って離散的な物体と接触する場合にも誘発される。このような接触は、粗い表面でしばしば観測される。応力-速度比は平均応力-速度比に置き換えることができ、平均応力は横方向の力を結晶の活性面積で割ったものであると仮定できる。

多くの場合、外部物体は非常に重いため、慣性のために結晶の高周波振動（MHz）に影響を与えない。その場合、水晶振動子は実験室のフレームに固定される。結晶表面が横方向に変位すると、接触によって結晶表面に復元力が働く。この応力は接点の数密度NSと平均バネ定数κSに比例する。バネ定数は複素数（κS* = κS’ + iκS’’）である場合があり、虚数部は結晶振動からのエネルギーの引き抜きを定量化する（例えば粘弾性効果による）。 このような状況では、小負荷近似は次のようになる。

これを応用することで、QCMを用いた複数のアスペリティ接触部のせん断剛性の非破壊検査が可能となる。

関連項目

[編集]

脚注

[編集]
  1. ^ 不均質な試料は、一般的には音響波の散乱を引き起こし、平均応力を計算するだけでは捉えることは出来ない.

参考文献

[編集]
  1. ^ “Piezoelectric sorption detector”. Analytical Chemistry 36 (9): 1735-1739. (August 1964). doi:10.1021/ac60215a012. 
  2. ^ a b c d e f g “発振法（QCM）”, 物性変化・分子間相互作用定量QCM装置 AFFINIXシリーズ - AFFINIX 原理, オリジナルの2019-06-10時点におけるアーカイブ。, https://web.archive.org/web/20190610074839/http://www.initium2000.com/technology/qcm.html 
  3. ^ “Verwendung von Schwingquarzen zur Wägung dünner Schichten und zur Mikrowägung” (ドイツ語). Zeitschrift für Physik (Springer-Verlag) 155 (2): 206-222. (April 1959). Bibcode: 1959ZPhy..155..206S. doi:10.1007/BF01337937. ISSN 0044-3328. オリジナルの2019-02-26時点におけるアーカイブ。. https://web.archive.org/web/20190226103453/http://jmfriedt.sequanux.org/t/sauerbrey.pdf 2019年2月26日閲覧。. 
  4. ^ 「広帯域1k～1.3GHz！10万円USBネットワーク・アナライザ VNWA3Eのすべて」第53巻第3号、CQ出版、2016年3月。 
  5. ^ 水晶振動子マイクロバランス（QCM）と電気化学水晶振動子マイクロバランス（EQCM）, http://www.bas.co.jp/xdata/electorode_photo/QCM_flowcell_kit2.pdf 
  6. ^ “Introduction, History, and Overview of Applications of Piezoelectric Quartz Crystal Microbalances”. Applications of Piezoelectric Quartz Crystal Microbalances. Methods and Phenomena. 7 (1 ed.). Amsterdam: Elsevier. (1984). pp. 1–393. doi:10.1016/B978-0-444-42277-4.50007-7. ISBN 978-0-444-42277-4. ISSN 0377-9025 
  7. ^ Arnau Vives, Antonio, ed (2004). Piezoelectric Transducers and Applications (1 ed.). Heidelberg: Springer-Verlag. ISBN 3-540-20998-0 
  8. ^ a b The Quartz Crystal Microbalance in Soft Matter Research - Fundamentals and Modeling. Soft and Biological Matter (1 ed.). Heidelberg: Springer International Publishing. (2015). Bibcode: 2015qcms.book.....J. doi:10.1007/978-3-319-07836-6. ISBN 978-3-319-07835-9. ISSN 2213-1736 
  9. ^ “Studying Soft Interfaces with Shear Waves: Principles and Applications of the Quartz Crystal Microbalance (QCM)”. Sensors 21 (10): 3490-3573. (May 2021). Bibcode: 2021Senso..21.3490J. doi:10.3390/s21103490. PMC 8157064. PMID 34067761. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC8157064/. 
  10. ^ “Acoustic Wave Microsensor Arrays for Vapor Sensing”. Chemical Reviews 100 (7): 627–648. (2000). doi:10.1021/cr980094j. PMID 11749298. 
  11. ^ Piezoelectric Sensors. Springer Series on chemical sensors and biosensors. 5. Heidelberg: Springer-Verlag. (2007). doi:10.1007/b100347. ISBN 978-3-540-36567-9. ISSN 1612-7617. LCCN 2006-935375. https://books.google.com/books?id=JchM7vvp8KMC 2019年3月1日閲覧。 
  12. ^ a b “Investigation of film-thickness determination by oscillating quartz resonators with large mass load”. Journal of Applied Physics 43 (11): 4385–4390. (November 1972). Bibcode: 1972JAP....43.4385L. doi:10.1063/1.1660931. 
  13. ^ “Experimental aspects of use of the quartz crystal microbalance in solution”. Electrochimica Acta 30 (10): 1295–1300. (October 1985). doi:10.1016/0013-4686(85)85005-2. 
  14. ^ “In Situ Interfacial Mass Detection with Piezoelectric Transducers”. Science 249 (4972): 1000–1007. (1990-08-31). Bibcode: 1990Sci...249.1000W. doi:10.1126/science.249.4972.1000. PMID 17789608. 
  15. ^ “Viscoelastic, mechanical, and dielectric measurements on complex samples with the quartz crystal microbalance”. Physical Chemistry Chemical Physics 10 (31): 4516–4534. (2008). Bibcode: 2008PCCP...10.4516J. doi:10.1039/b803960g. PMID 18665301. 
  16. ^ “Pulse mode shear horizontal-surface acoustic wave (SH-SAW) system for liquid based sensing applications”. Biosensors & Bioelectronics 19 (6): 627–632. (2004-01-15). doi:10.1016/S0956-5663(03)00257-4. PMID 14683647. http://irep.ntu.ac.uk/id/eprint/3840/1/195888_52%20Newton%20Preprint%20WM.pdf. 
  17. ^ “Review of shear surface acoustic waves in solids”. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control 45 (4): 935–938. (July 1998). doi:10.1109/58.710563. ISSN 0885-3010. PMID 18244248. 
  18. ^ “A Love plate biosensor utilising a polymer layer”. Sensors and Actuators B: Chemical（） 6 (1–3): 131–137. (January 1992). doi:10.1016/0925-4005(92)80044-X. 
  19. ^ “Measurement of Dynamic Shear Viscosity and Stiffness of Viscous Liquids by Means of Traveling Torsional Waves”. Journal of the Acoustical Society of America 24 (4): 355–. (1952). Bibcode: 1952ASAJ...24..355M. doi:10.1121/1.1906904. 
  20. ^ a b “An instrument for precise measurement of viscoelastic properties of low viscosity dilute macromolecular solutions at frequencies from 20 to 500 kHz”. Journal of Rheology 38 (4): 1195–. (1998-06-04). Bibcode: 1994JRheo..38.1195S. doi:10.1122/1.550608. 
  21. ^ “Basic Technology of Quartz Crystal Resonators”. Fortiming Corporation (2008年). 2018年8月27日時点のオリジナルよりアーカイブ。2019年3月3日閲覧。
  22. ^ “Langasite for high-temperature bulk acoustic wave applications”. Applied Physics Letters 78 (7): 976-. (2001-02-05). Bibcode: 2001ApPhL..78..976F. doi:10.1063/1.1345797. 
  23. ^ “GaPO4 Sensors for Gravimetric Monitoring during Atomic Layer Deposition at High Temperatures”. Analytical Chemistry 77 (11): 3531-3535. (2005-04-16). doi:10.1021/ac050349a. PMID 15924385. 
  24. ^ “Chemical sensors based on electrically sensitive quartz resonators”. Sensors and Actuators B: Chemical（） 91 (1–3): 320-325. (2003-06-01). doi:10.1016/S0925-4005(03)00094-7. 
  25. ^ a b IEC standard 60444-1
  26. ^ a b “The Role of Longitudinal Waves in Quartz Crystal Microbalance Applications in Liquids”. Analytical Chemistry 67 (4): 685–693. (February 1995). doi:10.1021/ac00100a001. 
  27. ^ “Method for measurement of shear-wave impedance in the MHz region for liquid samples of approximately 1 ml”. Journal of Physics E: Scientific Instruments 20 (5): 523–. (1987). Bibcode: 1987JPhE...20..523E. doi:10.1088/0022-3735/20/5/011. 
  28. ^ The Art of Electronics (2 ed.). New York: Cambridge University Press. (1989). ISBN 0-521-37095-7. OCLC 19125711 
  29. ^ a b “Circuit for continuous motional series resonant frequency and motional resistance monitoring of quartz crystal resonators by parallel capacitance compensation”. Review of Scientific Instruments 73 (7): 2724–. (2002-06-21). Bibcode: 2002RScI...73.2724A. doi:10.1063/1.1484254. 
  30. ^ a b “Impedance Analysis of Quartz Oscillators, Contacted on One Side with a Liquid”. Berichte der Bunsengesellschaft für Physikalische Chemie 92 (11): 1363–1368. (November 1988). doi:10.1002/bbpc.198800327. 
  31. ^ “A simple setup to simultaneously measure the resonant frequency and the absolute dissipation factor of a quartz crystal microbalance”. Review of Scientific Instruments 67 (9): 3238–3241. (1998-06-04). Bibcode: 1996RScI...67.3238R. doi:10.1063/1.1147494. 
  32. ^ “Method for Determining the Viscoelastic Properties of Dilute Polymer Solutions at Audio-Frequencies”. Journal of Applied Physics 25 (10): 1312–1320. (1954). Bibcode: 1954JAP....25.1312S. doi:10.1063/1.1721552. 
  33. ^ Introduction to Quartz Crystal Unit Design. New York: Van Nostrand Reinhold. (1982). ISBN 9780442262013. https://archive.org/details/introductiontoqu0000bott 
  34. ^ “The quartz crystal microbalance radial/polar dependence of mass sensitivity both on and off the electrodes”. Measurement Science and Technology 1 (7): 544–555. (1990). Bibcode: 1990MeScT...1..544C. doi:10.1088/0957-0233/1/7/002. 
  35. ^ “Who needs Crystal Devices?”. Epson Toyocom Corporation (2007年3月22日). 2007年7月18日時点のオリジナルよりアーカイブ。2007年5月30日閲覧。
  36. ^ “What do you mean by a crystal cut?”. Quartz Crystal FAQs. International Crystal Manufacturing Co., Inc. (ICM) (2007年). 2016年3月3日時点のオリジナルよりアーカイブ。2007年5月30日閲覧。
  37. ^ IEEE Transactions on Sonics and Ultrasonics 26: 163–. (1979).  (NB. Possible mixup of sources? While all three authors and the journal exist (and they published elsewhere in this journal), the existence of this particular article needs to be verified as it could not be found in online repositories so far.)
  38. ^ “The Quartz Microbalance: A Novel Approach to the In-Situ Investigation of Interfacial Phenomena at the Solid/Liquid Junction [New Analytical Methods (40)]”. Angewandte Chemie International Edition in English 29 (4): 329–. (April 1990). doi:10.1002/anie.199003293. 
  39. ^ “An in situ weighing study of the mechanism for the formation of the adsorbed oxygen monolayer at a gold electrode”. Journal of Electroanalytical Chemistry and Interfacial Electrochemistry 188 (1–2): 131–136. (1985-06-25). doi:10.1016/S0022-0728(85)80057-7. 
  40. ^ “Measurement of interfacial processes at electrode surfaces with the electrochemical quartz crystal microbalance”. Chemical Reviews 92 (6): 1335–1379. (September 1992). doi:10.1021/cr00014a006. 
  41. ^ “Studies of Viscoelasticity with the QCM”. Piezoelectric Sensors. Springer Series on Chemical Sensors and Biosensors. 5 (1 ed.). Berlin / Heidelberg: Springer-Verlag. (2007) (2006-09-08発行). pp. 49–109. doi:10.1007/5346_024. ISBN 978-3-540-36567-9. ISSN 1612-7617. LCCN 2006-935375. https://books.google.com/books?id=JchM7vvp8KMC&pg=PA48 2019年3月1日閲覧。 
  42. ^ “Chapter 36”. Mechanics of Solids - Waves in Elastic and Viscoelastic Solids (Theory and Experiment). IV (new revised ed.). Heidelberg: Springer-Verlag. (1984-07-02). pp. 257–. ISBN 0-38713163-9. https://books.google.com/books?id=JikIAQAAIAAJ 2019年3月1日閲覧。  (NB. Originally published as volume VIa/4 of Encyclopedia of Physics（ドイツ語版）.)
  43. ^ “Physical description of a viscoelastically loaded AT-cut quartz resonator”. Journal of Applied Physics 68 (5): 1993–. (1990). Bibcode: 1990JAP....68.1993R. doi:10.1063/1.346548. 
  44. ^ “Viscoelastic properties of thin films probed with a quartz-crystal resonator”. Physical Review B 46 (12): 7808–7815. (1992-09-15). Bibcode: 1992PhRvB..46.7808J. doi:10.1103/PhysRevB.46.7808. PMID 10002521. 
  45. ^ “High frequency tribological investigations on quartz resonator surfaces”. Journal of Applied Physics 85 (7): 3759–. (1999-03-22). Bibcode: 1999JAP....85.3759L. doi:10.1063/1.369745. 
  46. ^ “Effect of sample heterogeneity on the interpretation of QCM data: comparison of combined quartz crystal microbalance/atomic force microscopy measurements with finite element method modeling”. Analytical Chemistry 80 (23): 8891–8899. (2008-10-28). doi:10.1021/ac8013115. PMID 18954085. 
  47. ^ “Derivation of the shear compliance of thin films on quartz resonators from comparison of the frequency shifts on different harmonics: A perturbation analysis”. Journal of Applied Physics 89 (11): 6356–. (2001-06-07). Bibcode: 2001JAP....89.6356J. doi:10.1063/1.1358317. 
  48. ^ “A Theory of a Quartz Crystal Microbalance Based upon a Mason Equivalent Circuit”. Japanese Journal of Applied Physics Part 1 29 (5): 963–969. (1990-03-17). Bibcode: 1990JaJAP..29..963N. doi:10.1143/JJAP.29.963. 
  49. ^ “Modeling the Responses of Thickness-Shear Mode Resonators under Various Loading Conditions”. Analytical Chemistry 71 (11): 2205–2214. (1999-04-28). doi:10.1021/ac981272b. PMID 21662758. 
  50. ^ “Role of Mass Accumulation and Viscoelastic Film Properties for the Response of Acoustic-Wave-Based Chemical Sensors”. Analytical Chemistry 71 (13): 2488–2496. (1999-05-21). doi:10.1021/ac981245l. PMID 21662792. 
  51. ^ “Improved quartz crystal microbalance technique”. Journal of Applied Physics 56 (3): 608–. (February 1984). Bibcode: 1984JAP....56..608B. doi:10.1063/1.333990. 
  52. ^ “Simultaneous Atomic Force Microscope and Quartz Crystal Microbalance Measurements: Interactions and Displacement Field of a Quartz Crystal Microbalance”. Japanese Journal of Applied Physics Part 1 41 (6A): 3974–3977. (2002-02-25). Bibcode: 2002JaJAP..41.3974F. doi:10.1143/JJAP.41.3974. 
  53. ^ Soviet Physics-Technical Physics (American Institute of Physics) 32: 325–. (1987). ISSN 0038-5662. OCLC 1911544.  (NB. V. V. Borovikov translates to В. В. Боровиков in Cyrillic.)
  54. ^ Piezoelectric Crystals and Their Applications to Ultrasonics. Bell Telephone Laboratories series (1 ed.). New York: D. Van Nostrand Company, Inc.. (1950). OCLC 608479473. ark:/13960/t4xh07b19. https://archive.org/details/piezoelectriccry00maso 2019年3月1日閲覧。 
  55. ^ “The oscillation frequency of a quartz resonator in contact with liquid”. Analytica Chimica Acta (Elsevier B.V.) 175: 99–105. (1985). Bibcode: 1985AcAC..175...99K. doi:10.1016/S0003-2670(00)82721-X. 
  56. ^ a b “Measurement of the viscosity of media by means of shear vibration of plane piezoresonators”. Instruments and Experimental Techniques 19 (1): 223–224. (January 1976). https://www.researchgate.net/publication/281196837 2019年2月28日閲覧。. 
  57. ^ “Characterization of a thickness-shear mode quartz resonator with multiple nonpiezoelectric layers”. Journal of Applied Physics 75 (3): 1319–. (1994). Bibcode: 1994JAP....75.1319G. doi:10.1063/1.356410. https://zenodo.org/record/1232916. 
  58. ^ “Characterization of a quartz crystal microbalance with simultaneous mass and liquid loading”. Analytical Chemistry 63 (20): 2272–2281. (October 1991). doi:10.1021/ac00020a015. 
  59. ^ “Swelling of a polymer brush probed with a quartz crystal resonator”. Physical Review E 56 (1): 680–. (1997-07-01). Bibcode: 1997PhRvE..56..680D. doi:10.1103/PhysRevE.56.680. 
  60. ^ “Viscoelastic Acoustic Response of Layered Polymer Films at Fluid-Solid Interfaces: Continuum Mechanics Approach”. Physica Scripta 59 (5): 391–. (1999). arXiv:cond-mat/9805266. Bibcode: 1999PhyS...59..391V. doi:10.1238/Physica.Regular.059a00391. 
  61. ^ “Operation of the Quartz Crystal Microbalance in Liquids: Derivation of the Elastic Compliance of a Film from the Ratio of Bandwidth Shift and Frequency Shift”. Langmuir 20 (7): 2809–2812. (2004). doi:10.1021/la035965l. PMID 15835157. 
  62. ^ “Viscoelastic analysis of organic thin films on quartz resonators”. Macromolecular Chemistry and Physics 200 (3): 501–. (1999-02-26). doi:10.1002/(SICI)1521-3935(19990301)200:3<501::AID-MACP501>3.0.CO;2-W. 
  63. ^ “Effect of Molecular Architecture of PDMAEMA–POEGMA Random and Block Copolymers on Their Adsorption on Regenerated and Anionic Nanocelluloses and Evidence of Interfacial Water Expulsion”. The Journal of Physical Chemistry B 119 (49): 15275–15286. (2015-12-10). doi:10.1021/acs.jpcb.5b07628. PMID 26560798. 
  64. ^ “Triggering Protein Adsorption on Tailored Cationic Cellulose Surfaces”. Biomacromolecules 15 (11): 3931–3941. (2014-11-10). doi:10.1021/bm500997s. PMID 25233035. 
  65. ^ “Strongly Stretched Protein Resistant Poly(ethylene glycol) Brushes Prepared by Grafting-To”. ACS Applied Materials & Interfaces 7 (14): 7505–7515. (2015-04-15). doi:10.1021/acsami.5b01590. PMID 25812004. 

外部リンク

[編集]
「https://ja.wikipedia.org/w/index.php?title=水晶振動子マイクロバランス&oldid=100053818」から取得