時間尺度微分積分学
数学における時間尺度微分積分学(じかんしゃくどびぶんせきぶんがく、英: time-scale calculus)は、微分積分学と和分差分学とを統一するもので、微分方程式の理論と差分方程式の理論とを統合した(連続と離散の入り混じった)力学系の研究の方法論を提供する。時間尺度微分積分学は、離散および連続データを同時にモデリングすることが要求される任意の分野において応用を持つ。この分野における新たな微分の定義は、実数全体を引数とする函数に作用したとき通常の意味での微分と同値になり、整数全体を引数とする函数に作用したとき前進差分と同値となるようなものとして与えられる。
歴史
[編集]時間尺度微分積分学は、1988年にドイツの数学者シュテファン・ヒルゲルが導入した[1]ものだが、同様のアイデアはそれ以前よりあり、少なくとも和と積分が統合されるリーマン–スティルチェス積分の導入にまで遡れる。
デルタ微分方程式
[編集](連続的な)微分方程式に関する多くの結果は極めて容易に(離散的な)差分方程式の対応する結果に読み替えることができるが、それに当てはまらない差分方程式に関する結果はその連続版の対応物とは大きくかけ離れているように見える[2]。時間尺度上のデルタ微分方程式 (dynamic equation; 動力学方程式、動態方程式) の研究は、そのような齟齬について明らかにし、微分方程式と差分方程式の間での二度手間を避ける手助けとなる。その一般的なアイデアは、未知函数の定義域がいわゆる「時間尺度」(あるいは「時間集合」)と呼ばれる実数直線の任意の閉部分集合である場合の、デルタ微分方程式に対する結果を証明することである。こうすることにより、得られた結果は(通常の連続的な結果を示す)実数全体 ℝ や(通常の離散的な結果を示す)整数全体 ℤ のみならず、より一般にカントール集合のような複雑な時間尺度に対しても適用できる。
そのような時間尺度上のデルタ微分法の中で最も知られた三種の例として、微分法・差分法・量子解析を挙げることができる。Dynamic equations on a time scale have a potential for applications, such as in population dynamics. For example, they can model insect populations that evolve continuously while in season, die out in winter while their eggs are incubating or dormant, and then hatch in a new season, giving rise to a non–overlapping population.
厳密な定義
[編集]時間尺度あるいは測度鎖 (measure chain) とは実数直線 ℝ の任意の閉部分集合のこととする。一般の時間尺度を表すのに 𝕋 がよく用いられる。
時間尺度として最もよく遭遇するふたつが、実数全体 ℝ や離散時間 hℤ である。
A single point in a time scale is defined as:
時間尺度上の演算
[編集]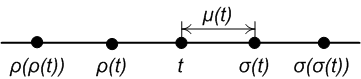
与えられた点 t に対して右または左にある最も近い時間尺度上の点を表す演算として「前方(前進)シフト」および「後方(後退)シフト」が定義される。式で書けば
- 前進シフト・前方跳躍:
- 後退シフト・後方跳躍:
さらに、粒度 (graininess) μ が、右方の最近接点への距離 として定義される。
時間尺度上の点の分類
[編集]
任意の点 t ∈ 𝕋 が、
- 左稠密 (left dense) であるとは ρ(t) = t なるときに言う;
- 右稠密 (right dense) であるとは σ(t) = t なるときに言う;
- 左散在 (left scattered) であるとは ρ(t) < t なるときに言う;
- 右散在 (right scattered) であるとは σ(t) > t なるときに言う;
- 稠密 (dense) であるとは左稠密かつ右稠密であるときに言う;
- 孤立 (isolated) しているとは左散在かつ右散在であるときに言う。
連続性
[編集]時間尺度の連続性は稠密性の同意語として再定義される。すなわち、時間尺度が点 t において右連続であるとは、それが t において右稠密であることを言い、同様に左連続であるとは左稠密であることを言う。
微分
[編集]時間尺度上の函数 をとる(ここでは簡単のため終域を実数直線 ℝ としたが、これは任意のバナッハ空間でよい)。
- 定義 (デルタ微分/ヒルゲル微分)
- f のデルタ微分が存在するとは、任意の ε > 0 に対し t の適当な近傍 U を選べば とできるときに言う。
- 𝕋 = ℝ と取れば、σ(t) = t かつ μ(t) = 0 であり、fΔ = f′ は通常の微分積分学で用いられる微分となる。
- 𝕋 = ℤ(整数全体)と取れば、σ(t) = t + 1 かつ μ(t) = 1 であり、fΔ = Δf は和分差分学で用いられる前進差分となる。
積分
[編集]デルタ微分に関する反微分(不定積分)としてデルタ積分が定義される。函数 F(t) が連続な導函数 f(t) := FΔ(t) を持つときには と置けばよい。
微分積分学における諸概念の時間尺度版
[編集]- ラプラス変換・z-変換
- 時間尺度上で定義された函数に対して、任意の時間尺度に対して同じ変換表を用いて、ラプラス変換を定義することができる。時間尺度上のラプラス変換は時間尺度上のデルタ微分方程式を解くことに利用できる。時間尺度が非負整数全体であるとき、この変換は修正z変換 に等しい[2]。
- 偏微分法
- 偏微分方程式と偏差分方程式は時間尺度上の偏デルタ微分方程式に統合される[3][4][5]。
- 重積分
- 時間尺度上の重積分は Bohner (2005) で扱われている[6]。
- 確率デルタ微分方程式
- 確率微分方程式と確率差分方程式は確率デルタ微分方程式に一般化される[7]。
- 測度論
- 各時間尺度に対して自然な測度 が付随する[8][9]。ただし、λ はルベーグ測度で、ρ は ℝ 上定義された後方シフト作用素とする。デルタ積分は、この測度に関する通常のルベーグ–スティルチェス積分 として理解でき、またデルタ微分はこの測度に関するラドン–ニコディム微分 となる[10]。
- 超函数
- ディラックのデルタとクロネッカーのデルタは、時間尺度上のヒルゲルのデルタ に統合される[11][12]。
- 積分方程式
- 積分方程式と和分方程式は、時間尺度上の積分方程式に統合される[13]。
- 分数階微積分
- 時間尺度上の分数階微分積分学は Bastos, Mozyrska & Torres (2010) が扱っている[14]。
脚注
[編集]出典
[編集]- ^ Hilger, Stefan (1998). Ein Maßkettenkalkül mit Anwendung auf Zentrumsmannigfaltigkeiten. Universität Würzburg.
- ^ a b Martin Bohner & Allan Peterson (2001). Dynamic Equations on Time Scales. Birkhäuser. ISBN 978-0-8176-4225-9
- ^ Ahlbrandt, Calvin D.; Morian, Christina (2002). “Partial differential equations on time scales”. Journal of Computational and Applied Mathematics 141: 35–55. Bibcode: 2002JCoAM.141...35A. doi:10.1016/S0377-0427(01)00434-4.
- ^ Partial dynamic equations on time scales, B Jackson – Journal of Computational and Applied Mathematics, 2006
- ^ Partial differentiation on time scales, M Bohner, GS Guseinov, Dynamic Systems and Applications 13 (2004) 351–379
- ^ Bohner, M; Guseinov, GS (2005). “Multiple integration on time scales”. Dynamic Systems and Applications.
- ^ STOCHASTIC DYNAMIC EQUATIONS, SUMAN SANYAL, 2008
- ^ Guseinov, GS (2003). “Integration on time scales”. J. Math. Anal. Appl. 285: 107–127. doi:10.1016/S0022-247X(03)00361-5.
- ^ Deniz, A (2007年). “Measure theory on time scales” (PDF). 2011年8月20日時点のオリジナルよりアーカイブ。2018年11月15日閲覧。
- ^ Eckhardt, J; Teschl, G (2012). “On the connection between the Hilger and Radon–Nikodym derivatives”. J. Math. Anal. Appl. 385: 1184–1189. arXiv:1102.2511. doi:10.1016/j.jmaa.2011.07.041.
- ^ The Laplace transform on time scales revisited, John M. Davis, Ian A. Gravagne , Billy J. Jackson , Robert J. Marks II , Alice A. Ramos, J. Math. Anal. Appl. 332 (2007) 1291–1307
- ^ Bilateral Laplace Transforms on Time Scales: Convergence, Convolution, and the Characterization of Stationary Stochastic Time Series Archived 2011-07-14 at the Wayback Machine., John M. Davis, Ian A. Gravagne and Robert J. Marks II
- ^ Volterra integral equations on time scales: Basic qualitative and quantitative results with applications to initial value problems on unbounded domains Archived 2009-09-13 at the Wayback Machine., Tomasia Kulik and Christopher C. Tisdell, 2007
- ^ Bastos, Nuno R. O.; Mozyrska, Dorota; Torres, Delfim F. M.. Fractional Derivatives and Integrals on Time Scales via the Inverse Generalized Laplace Transform. arXiv:1012.1555. Bibcode: 2010arXiv1012.1555B.
関連項目
[編集]- フラクタル上の解析学: カントール集合上のデルタ微分方程式
参考文献
[編集]- Dynamic equations on time scales: a survey, Ravi Agarwal, Martin Bohner, Donal O’Regan, Allan Peterson, Journal of Computational and Applied Mathematics 141 (2002) 1–26
関連文献
[編集]- The Baylor University Time Scales Group
- Dynamic Equations on Time Scales Special issue of Journal of Computational and Applied Mathematics (2002)
- Dynamic Equations And Applications Special Issue of Advances in Difference Equations (2006)
- Dynamic Equations on Time Scales: Qualitative Analysis and Applications Special issue of Nonlinear Dynamics And Systems Theory (2009)
- Timescalewiki.org












![{\displaystyle {\mathcal {Z}}'\{x[z]\}={\frac {{\mathcal {Z}}\{x[z+1]\}}{z+1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0eff16581e442c4142fd193357778ff342911e5)



