恒星の自転

恒星の自転(こうせいのじてん、英: Stellar rotation)は、恒星の自身の自転軸の周りでの角運動である。自転速度は、恒星のスペクトルや表面上の構造の動きのタイミングから測定することができる。
恒星の自転は、遠心力により赤道上の膨らみを生み出す。恒星は固体ではないため、差動運動も見られる。そのため、恒星の赤道は、高緯度地域とは異なる角速度で運動できる。このような恒星内の速度の差が恒星磁場を生み出す原因の1つとなる[1]。
恒星磁場は、恒星風と相互作用する。恒星から恒星風が吹くことで、自転の角速度は遅くなる。恒星磁場は恒星風と相互作用し、恒星の自転の障害となる。結果として、角運動量は恒星から恒星風へと輸送され、時間が経過すると恒星の自転速度は徐々に遅くなる。
測定
[編集]恒星を極方向から観測するのでない限り、恒星表面の一部分は、いくらか観測者から遠ざかったり近づいたりする。観測者の方向に向かう運動の成分は、視線速度と呼ばれる。視線速度が観測者に向かってくる方向の場合、ドップラー効果により放射の周波数は高くなる。逆に観測者から遠ざかる方向の場合は、周波数は低くなる。恒星の吸収線が観測される時には、このシフトにより、線の幅は広くなる[2]。しかし、この広がりは、線の幅を広げる他の効果とは区別することができる。
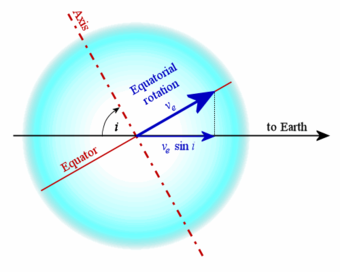
線の広がりで観測される視線速度の成分は、自転軸と視線との傾斜角に依存する。この値は、で表され、ここでveは赤道上での自転速度、iは傾斜角である。しかし、iは常に既知ではなく、そのため、恒星の自転速度の最小値が与えられる。つまり、iが直角ではない場合、真の自転速度は、より大きい[2]となる。この値は、推定自転速度と呼ばれる場合もある。
巨星では、恒星大気の微視的乱流が吸収線の広がりに与える効果は自転による効果よりもずっと大きいが、重力レンズ効果を用いる別の方法を採ることができる。重力レンズ効果は、大質量の天体がより遠くの天体の前面を通過する時に起こり、レンズのような役割を果たして一時的に像が大きくなる。この方法で集められたより詳細な情報により、微視的乱流と自転の効果を区別することができる[3]。
恒星表面に、恒星黒点のような磁場活動がある場合、それらの特徴から自転速度を推定することができる。しかし、それらの特徴は赤道以外にも現れることがあり、また緯度上を移動することもあるため、恒星の差動運動が測定値を変化させることがある。恒星の磁場活動は、しばしば高速の自転と関わっており、そのためこの技術は、そのような恒星の測定のために用いられる[4]。観測により、磁場が恒星中のガスの流れを変更することで、恒星黒点が実際に恒星の自転速度を変化させることが示された[5]。
物理的効果
[編集]赤道上の膨らみ
[編集]重力のため、全ての質量は重力中心にできるだけ近くに集まろうとし、天体は完全な球形に収縮する。しかし、自転する恒星は球形ではなく、赤道部分に膨らみを持つ。
自転する原始星円盤は収縮してより球形に近い恒星を形成するが、収縮により完全な球形にはならない。極では、全ての重力が収縮に働くが、赤道上では実効重力は遠心力に相殺される。星形成後の恒星の最終的な形は、赤道領域の実効重力がそれ以上恒星を中心に引っ張れないという意味で均衡形に達する。また自転により赤道では、フォン・ツァイペルが記述したような重力減光が起きる。
赤道上の膨らみの極端な例は、レグルスAで見られる。この恒星の赤道上での自転速度は、317 ± 3 km/sと測定された。この値は、15.9時間の自転周期に相当し、恒星が自壊する速度の86%に達する。赤道半径は、極方向の半径よりも32%大きい[6]。高速で自転する恒星には、他にさいだん座α星、おうし座28番星、ベガ、アケルナル等がある。
恒星が自壊する速度とは、赤道上の遠心力が重力と釣り合った時を意味する。安定な恒星の自転速度は、必ずこの値以下である[7]。
差動運動
[編集]恒星表面の差動運動は、太陽のような恒星で、緯度によって異なる角速度として観測される。通常、角速度は緯度が上がるにつれて低下する。しかし、HD 31993等では、その逆も観測されている[8][9]。太陽以外で最初に差動運動が詳細にマッピングされたのは、かじき座AB星である[1] [10]。
差動運動を引き起こす機構は、恒星内部の対流の乱流である。対流は、プラズマの質量運動に乗ってエネルギーを恒星表面に運ぶ。このプラズマ質量は、恒星の角速度の一部も運ぶ。乱流が発生すると、角モーメントは子午線流に乗って異なる緯度に再分配される[11][12]。
自転速度の分布の比較的はっきりした境界は、恒星磁場を生み出すダイナモが効率的に現れる場所であると信じられている。恒星の自転の分布と磁場の間には、複雑な相互作用があり、磁気エネルギーが運動エネルギーに変換され、速度分布を変化させている[1]。
自転の減速
[編集]恒星は、低温のガスや塵の雲が重力崩壊した結果できると信じられている。雲が崩壊すると、角モーメントの保存により雲の自転速度は増加し、周囲の物質を回転円盤に集める。この円盤の密度の高い中心部で原始星が形成され、崩壊の重力エネルギーで熱を持つ。
崩壊が進行すると、降着する原始星が赤道での遠心力により自壊する速度まで、自転速度が増加する。そのため、自転速度は最初の10万年の間に減速する。減速の機構についての1つの可能な説明は、原始星の磁場と恒星風の相互作用による磁気ブレーキである。増大する恒星風が角モーメントを運び去り、原始星の自転速度を減速させる[13][14]。
| スペクトル型 | ve (km/s) |
|---|---|
| O5 | 190 |
| B0 | 200 |
| B5 | 210 |
| A0 | 190 |
| A5 | 160 |
| F0 | 95 |
| F5 | 25 |
| G0 | 12 |
スペクトル型がO5からF5の間のほとんどの主系列星は、高速で自転していることが分かっている[6][16]。この範囲にある恒星は、質量とともに自転速度が増大する。自転速度は、若くて質量の大きいB型主系列星で最大となる。恒星の寿命は、質量の増加とともに短くなるが、これは恒星の年齢に伴う自転速度の減少で説明することができる。
主系列星では、自転速度の減少は次の数学的関係で近似できる。
ここで、は赤道上の角速度、tは恒星の年齢である[17]。この関係は、1972年に発見したAndrew P. Skumanichの名前に因んでSkumanichの法則と呼ばれる[18]。Gyrochronologyは、太陽で校正を行い、自転速度に基づいて恒星の年齢を決定する学問である[19]。
恒星は、光球から恒星風を放出してゆっくりと質量が減少する。恒星の磁場は、放出物質にトルクを与え、角モーメントを継続的に恒星から転移している。自転速度が15km/sよりも速い恒星は、質量喪失がより速く、従って自転速度の減少もより速く進行する。恒星の自転が遅くなると、角モーメントの減少速度も遅くなる。このような条件下では、恒星は徐々に自転ゼロの状態に近づくが、決してその状態に達することはない[20]。
近接連星
[編集]2つの恒星が、自身の直径と同程度の距離だけ離れてお互いの周りを公転すると、近接連星となる。このような距離では、潮汐効果、質量転移、さらには衝突等のより複雑な相互作用が生じうる。近接連星の潮汐相互作用は、軌道及び自転のパラメータを変化させる。系の合計の角モーメントは保存されるが、角モーメントは軌道周期と自転速度の間で転移されうる[21]。
近接連星の一方の恒星は、重力相互作用によってもう一方に潮汐を起こさせる。しかし、それによる膨らみは重力の方向と若干揃わなくなり、重力がトルクを生じ、角モーメントが転移される。これらの作用により、系は進化し、安定な平衡状態に達する。自転軸が軌道平面に垂直でない場合は、この作用はさらに複雑になる[21]。
接触連星や半分離連星の場合は、質量転移によりかなりの角モーメントが転移される。降着を受ける伴星は自転速度が増加し、赤道から質量を放出する[22]。
縮退星
[編集]恒星が熱核融合によるエネルギー生産を終了すると、より小型の縮退状態に進化する。この過程の間、恒星の直径はかなり収縮し、それに対応して角速度は増加する。
白色矮星
[編集]白色矮星は、かつての熱核融合の生成物で構成されているが、それらの重い元素を燃やす程の質量を持たない恒星である。電子縮退圧と呼ばれる量子効果で支えられており、それ以上崩壊することはない。通常、元になる恒星が外層を失った際の角モーメントの喪失により、ほとんどの白色矮星の自転速度は遅い[23]。
ゆっくり自転する白色矮星は、中性子星に崩壊するかIa型超新星爆発を起こす以外は、チャンドラセカール限界の1.44太陽質量を超えられない。降着や衝突により、白色矮星がこの質量に達すると、重力が電子による圧力を超える。しかし、白色矮星が高速で自転していると、赤道地域の実効重力は減少し、白色矮星はチャンドラセカール限界を超えることができる。このような高速の自転は、例えば質量降着による角モーメントの転移等によって実際に起こりうることである[24]。
中性子星
[編集]
中性子星は、主に中性子で構成される非常に密度の大きい恒星の残骸である。中性子星の質量は、1.35から2.1太陽質量の範囲である。恒星の崩壊によって新しく形成される中性子星は、1秒間に数百回転という非常に速い自転速度を持つ。
パルサーは、磁場を持って自転する中性子星である。パルサーの極からは、高い指向性を持つ電磁放射のビームが放出される。ビームが太陽系の方向に向くと、パルサーは、周期的なパルスとして観測される。磁場から放射されるエネルギーは、徐々に自転速度を減少させる。そのため、古いパルサーのパルスの間隔は数秒にもなる[25]。
ブラックホール
[編集]ブラックホールは、光が逃げられないほど強力な重力場を持つ天体である。自転する恒星の崩壊によってブラックホールが形成された場合、放出されたガスによって喪失した分以外の全ての角モーメントが保持される。この自転は、「作用圏」と呼ばれる、ブラックホールに引っ張られる偏球形の空間を作り出す。この空間に落ち込んだ質量はエネルギーを獲得し、質量の一部は外側に放出される。質量が放出されると、ブラックホールは角モーメントを失う(ペンローズ過程を参照)[26]。ブラックホールの自転速度は、光速の98.7%にも達すると測定されている[27]。
出典
[編集]- ^ a b c Donati, Jean-Francois (November 5, 2003). “Differential rotation of stars other than the Sun”. Laboratoire d’Astrophysique de Toulouse. 2007年6月24日閲覧。
- ^ a b Shajn, G.; Struve, O. (1929). “On the rotation of the stars”. Monthly Notices of the Royal Astronomical Society 89: 222-239. Bibcode: 1929MNRAS..89..222S.
- ^ Gould, Andrew (1997). “Measuring the Rotation Speed of Giant Stars from Gravitational Microlensing”. Astrophysical Journal 483 (1): 98-102. arXiv:astro-ph/9611057. Bibcode: 1996astro.ph.11057G. doi:10.1086/304244.
- ^ Soon, W.; Frick, P.; Baliunas, S. (1999). “On the rotation of the stars”. The Astrophysical Journal 510 (2): L135-L138. arXiv:astro-ph/9811114. Bibcode: 1999ApJ...510L.135S. doi:10.1086/311805.
- ^ Collier Cameron, A.; Donati, J.-F. (2002). “Doin' the twist: secular changes in the surface differential rotation on AB Doradus”. Monthly Notices of the Royal Astronomical Society 329 (1): L23-L27. arXiv:astro-ph/0111235. Bibcode: 2002MNRAS.329L..23C. doi:10.1046/j.1365-8711.2002.05147.x.
- ^ a b McAlister, H. A., ten Brummelaar, T. A., et al. (2005). “First Results from the CHARA Array. I. An Interferometric and Spectroscopic Study of the Fast Rotator Alpha Leonis (Regulus).”. The Astrophysical Journal 628 (1): 439-452. arXiv:astro-ph/0501261. Bibcode: 2005ApJ...628..439M. doi:10.1086/430730.
- ^ Hardorp, J.; Strittmatter, P. A. (8–11 September 1969). "Rotation and Evolution of be Stars". Proceedings of IAU Colloq. 4. Ohio State University, Columbus, Ohio: Gordon and Breach Science Publishers. p. 48. Bibcode:1970stro.coll...48H。
- ^ Kitchatinov, L. L.; Rudiger, G. (2004). “Anti-solar differential rotation”. Astronomische Nachrichten 325 (6): 496-500. arXiv:astro-ph/0504173. Bibcode: 2004AN....325..496K. doi:10.1002/asna.200410297.
- ^ Ruediger, G.; von Rekowski, B.; Donahue, R. A.; Baliunas, S. L. (1998). “Differential Rotation and Meridional Flow for Fast-rotating Solar-Type Stars”. Astrophysical Journal 494 (2): 691-699. Bibcode: 1998ApJ...494..691R. doi:10.1086/305216.
- ^ Donati, J.-F.; Collier Cameron, A. (1997). “Differential rotation and magnetic polarity patterns on AB Doradus”. Monthly Notices of the Royal Astronomical Society 291 (1): 1-19. Bibcode: 1997MNRAS.291....1D.
- ^ Korab, Holly (June 25, 1997). “NCSA Access: 3D Star Simulation”. National Center for Supercomputing Applications. 2007年6月27日閲覧。
- ^ Kuker, M.; Rudiger, G. (2004). “Differential rotation on the lower main sequence”. Astronomische Nachrichten 326 (3): 265-268. arXiv:astro-ph/0504411. Bibcode: 2005AN....326..265K. doi:10.1002/asna.200410387.
- ^ Ferreira, J.; Pelletier, G.; Appl, S. (2000). “Reconnection X-winds: spin-down of low-mass protostars”. Monthly Notices of the Royal Astronomical Society 312 (2): 387-397. Bibcode: 2000MNRAS.312..387F. doi:10.1046/j.1365-8711.2000.03215.x.
- ^ Devitt, Terry (January 31, 2001). “What Puts The Brakes On Madly Spinning Stars?”. University of Wisconsin-Madison 2007年6月27日閲覧。
- ^ McNally, D. (1965). “The distribution of angular momentum among main sequence stars”. The Observatory 85: 166-169. Bibcode: 1965Obs....85..166M.
- ^ Peterson, Deane M.; et al. (2004). "Resolving the effects of rotation in early type stars". New Frontiers in Stellar Interferometry, Proceedings of SPIE Volume 5491. Bellingham, Washington, USA: The International Society for Optical Engineering. p. 65. Bibcode:2004SPIE.5491...65P。
- ^ Tassoul, Jean-Louis (1972). Stellar Rotation. Cambridge, MA: Cambridge University Press. ISBN 0-521-77218-4 2007年6月26日閲覧。
- ^ Skumanich, Andrew P. (1972). “Time Scales for CA II Emission Decay, Rotational Braking, and Lithium Depletion”. The Astrophysical Journal 171: 565. Bibcode: 1972ApJ...171..565S. doi:10.1086/151310.
- ^ Barnes, Sydney A. (2007). “Ages for illustrative field stars using gyrochronology: viability, limitations and errors”. The Astrophysical Journal 669 (2): 1167-1189. arXiv:0704.3068. Bibcode: 2007ApJ...669.1167B. doi:10.1086/519295.
- ^ Nariai, Kyoji (1969). “Mass Loss from Coronae and Its Effect upon Stellar Rotation”. Astrophysics and Space Science 3 (1): 150-159. Bibcode: 1969Ap&SS...3..150N. doi:10.1007/BF00649601.
- ^ a b Hut, P. (1999). “Tidal evolution in close binary systems”. Astronomy and Astrophysics 99 (1): 126-140. Bibcode: 1981A&A....99..126H.
- ^ Weaver, D.; Nicholson, M. (December 4, 1997). “One Star's Loss is Another's Gain: Hubble Captures Brief Moment in Life of Lively Duo”. NASA Hubble. 2007年7月3日閲覧。
- ^ Willson, L. A.; Stalio, R. (1990). Angular Momentum and Mass Loss for Hot Stars (1st ed.). Springer. pp. 315-16. ISBN 0-7923-0881-6
- ^ Yoon, S.-C.; Langer, N. (2004). “Presupernova evolution of accreting white dwarfs with rotation”. Astronomy and Astrophysics 419 (2): 623-644. arXiv:astro-ph/0402287. Bibcode: 2004A&A...419..623Y. doi:10.1051/0004-6361:20035822.
- ^ Lorimer, D. R. (1998年8月28日). “Binary and Millisecond Pulsars”. Max-Planck-Gesellschaft. 2012年5月1日時点のオリジナルよりアーカイブ。2007年6月27日閲覧。
- ^ Begelman, Mitchell C. (2003). “Evidence for Black Holes”. Science 300 (5627): 1898-1903. Bibcode: 2003Sci...300.1898B. doi:10.1126/science.1085334. PMID 12817138.
- ^ Tune, Lee (May 29, 2007). “Spin of Supermassive Black Holes Measured for First Time”. University of Maryland Newsdesk 2007年6月25日閲覧。
外部リンク
[編集]- Staff (February 28, 2006). “Stellar Spots and Cyclic Activity: Detailed Results”. ETH Zurich. 2009年10月22日閲覧。[リンク切れ]



