中心つき八角数
表示
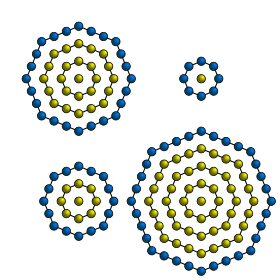
中心つき八角数(ちゅうしんつきはちかくすう、Centered octagonal number)は、八角形の中心つき多角数である。中心の点を取り巻くように正八角形の形に点を並べた時の点の総数である[1]。中心つき八角数は、奇数の平方数と同じである[2]。従って、n 番目の中心つき八角数は、以下の式で与えられる。
最初のいくつかの中心つき八角数は、次の通りである[2]。
- 1, 9, 25, 49, 81, 121, 169, 225, 289, 361, 441, 529, 625, 729, 841, 961, 1089,… (オンライン整数列大辞典の数列 A016754)
中心つき八角数のラマヌジャンのタウ函数を計算すると、奇数になる。その他全ての数では、偶数になる[2]。
出典
[編集]- ^ Teo, Boon K.; Sloane, N. J. A. (1985), “Magic numbers in polygonal and polyhedral clusters”, Inorganic Chemistry 24: 4545–4558, doi:10.1021/ic00220a025.
- ^ a b c Sloane, N.J.A. (ed.). "Sequence A016754 (Odd squares: (2n+1)^2. Also centered octagonal numbers.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
{{cite web}}: Cite webテンプレートでは|access-date=引数が必須です。 (説明)

