ヴィタリの被覆定理

数学において、ヴィタリの被覆定理（ヴィタリのひふくていり、Vitali covering lemma）は、ユークリッド空間の測度論でよく使われる組み合わせ幾何学における結果である。この定理の中間ステップにあたるヴィタリの被覆補題も独立して興味深い結果とされている。被覆定理はイタリアの数学者ジュゼッペ・ヴィタリに由来する。 この定理はどんな R^d の部分集合 E も E のヴィタリ被覆から取り出された互いに素な族によって、高々ルベーグ測度0の集合を残すまで被覆できることを主張する。

ヴィタリの被覆補題

$\mathbb {R} ^{1}$ における補題の可視化。

上図: 球の集まり; 緑の球は互いに素な部分族。下図: 緑の球を3倍半径にしたもので青も含めて全ての球が覆われている。

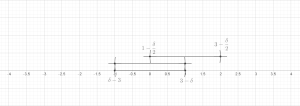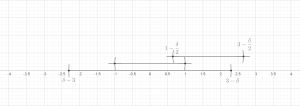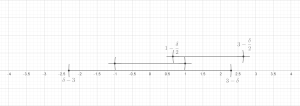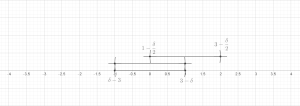
被覆補題には2つの基本的なバージョンがある、有限バージョンと無限バージョンである。この両方の補題は一般的な距離空間の設定で証明されるが、通常、これらの結果はユークリッド空間 $\mathbb {R} ^{d}$ の特別な場合に適用される。これらの定理において、ここでは次の表記を用いる: ${\textstyle B=B(x,r)}$ が球体で $c\in \mathbb {R}$ なら $cB$ で球体 ${\textstyle B(x,cr)}$ を表す。

有限バージョン

定理 (有限被覆補題). 距離空間において $B_{1},\dots ,B_{n}$ を有限個の球体からなる族とする。このとき、その部分族 $B_{j_{1}},B_{j_{2}},\dots ,B_{j_{m}}$ であってそれらが互いに素であって、 $$B_{1}\cup B_{2}\cup \dots \cup B_{n}\subseteq 3B_{j_{1}}\cup 3B_{j_{2}}\cup \dots \cup 3B_{j_{m}}.$$ を満たすものがとれる。

証明: 一般性を失うことなく、球体の族は空でないとしてよい; すなわち、n > 0とする。$B_{j_{1}}$ を最大半径の球体とする。帰納的に、$B_{j_{1}},\dots ,B_{j_{k}}$ が選ばれていると仮定する。もし$B_{1},\dots ,B_{n}$に属する球体で$B_{j_{1}}\cup B_{j_{2}}\cup \dots \cup B_{j_{k}}$と互いに素なものがあったら、そのうち最大の半径を持つものを$B_{j_{k+1}}$と定める（同順位のものはどれでもよい）。互いに素なものがなかったら、m := k と定めて帰納的定義を終了する。

そこで${\textstyle X:=\bigcup _{k=1}^{m}3\,B_{j_{k}}}$と定める。あとは各 $i=1,2,\dots ,n$ について $B_{i}\subset X$ となっていることを示せばよい。$i\in \{j_{1},\dots ,j_{m}\}$のときは自明。そうでないとき、ある $k\in \{1,\dots ,m\}$ で $B_{i}$ が $B_{j_{k}}$ と交わっているものがあることになる。そのような最小の $k$ を選ぶとこのとき $B_{j_{k}}$ の半径は少なくとも $B_{i}$ の半径以上であることに注意する。三角不等式によって、$B_{i}\subset 3\,B_{j_{k}}\subset X$ が導かれ、これが求めていたものである。これで有限バージョンの証明が完了した。

無限バージョン

定理 (無限被覆補題). $\mathbf {F}$ を可分距離空間における球体の任意の集合族であって、$$R:=\sup \,\{\mathrm {rad} (B):B\in \mathbf {F} \}<\infty$$ であるものとする。ここで $\mathrm {rad} (B)$ は球体 B の半径を表す。このとき、可算な部分集合族 $\mathbf {G} \subset \mathbf {F}$ であって次のことを満たすものが存在する: $\mathbf {G}$ の元は互いに素であり、各 $B\in \mathbf {F}$ はある $C\in \mathbf {G}$ と交わり $B\subset 5C$ を満たし、それにより $$\bigcup _{B\in \mathbf {F} }B\subseteq \bigcup _{C\in \mathbf {G} }5\,C.$$ となる。

証明: F を部分族 F_n, n ≥ 0 に次のようにして分割することを考える:

$\mathbf {F} _{n}=\{B\in \mathbf {F} :2^{-n-1}R<{\text{rad}}(B)\leq 2^{-n}R\}.$

列 G_n (ただし G_n ⊂ F_n)を次のように帰納的に定義する: 最初に、H₀ = F₀ とし、G₀ を H₀ の互いに素な部分集合族で極大なものとする。(このような部分集合族はツォルンの補題によって取れる). G₀,...,G_n が既に選ばれているとして、

$\mathbf {H} _{n+1}=\{B\in \mathbf {F} _{n+1}:\ B\cap C=\emptyset ,\ \ \forall C\in \mathbf {G} _{0}\cup \mathbf {G} _{1}\cup \dots \cup \mathbf {G} _{n}\},$

と定義し、G_n+1 はH_n+1の互いに素な部分集合族で極大なものとする。F の部分集合族

$\mathbf {G} :=\bigcup _{n=0}^{\infty }\mathbf {G} _{n}$

は定理の要求を満たしている: G は互いに素であり、与えられている距離空間が可分なので可算な族である。そしてこのとき、任意の球体 B ∈ F はある球体 C ∈ G と交わり B ⊂ 5C にもなっている。
というのも、$B\in \mathbf {F}$ が与えられたとき、B はある n についての F_n に属する。ここで B が H_n に属していない場合, n > 0 かつ B は G₀, ..., G_n−1 の和から取ったある球体と交わる。B ∈ H_n の場合は G_n の極大性により、B は G_n に属するある球体と交わる。どちらの場合でも、B は G₀, ..., G_n の和に属するある球体 C と交わる。その球体 C は半径が 2⁻ⁿ⁻¹R より大きい。B の半径は 2⁻ⁿR 以下なので、三角不等式によって B ⊂ 5C が言える。これが求めていたものであった。

注意

• 無限バージョンの証明は可分な距離空間で行ったが、可分な距離空間では互いに素な球体の族は必ず高々可算となる。可分でない空間において同様の議論を進めても互いに素な球体の部分族は得られるが、その場合はそれが可算になるとは限らない。
• 定理の結果は球体の半径を有界にしておかないと成り立たない: 中心がR^dの原点 0 である球体全ての集まりを考える; ここから互いに素な集合族を作ろうとしても一つの球体しかとることができない。それを B としても 5 B で最初の球体全てを覆うことはできない。
• 5 という定数は最適のものというわけではない。F_n を定義するときのスケール 2⁻ⁿ を c⁻ⁿ(c > 1) に変更すれば、最後の値は 5 ではなく 1 + 2c を用いることができる。つまり 3 より大きい全ての定数で補題は成立する、ただしちょうど 3 では成立しない。
• さらに詳しく分析すると、最初の F が R^d の部分集合 E の ヴィタリ被覆 であったとき、上の証明で定義される G は E を高々ルベーグ零集合を残すまで被覆できる。

応用と使い方

ヴィタリの補題の応用の一つはハーディ＝リトルウッドの極大不等式の証明である。この証明のように、ヴィタリの補題は次のような場合に良く使われる。例えば、d-次元ルベーグ測度 $\lambda _{d}$ を E ⊂ R^d に考えるとして、それがある球体の集まり $\{B_{j}:j\in J\}$ の和に含まれているなどして、より計算しやすい測度を持つまたは利用したい特別な性質を持つ場合である。もし、和の測度が計算できるなら E の測度の上界が分かる。しかしながら、互いに交わりを持つ集合の和の測度を計算するのは難しい。ヴィタリの補題によれば、互いに素な部分族 $\left\{B_{j}:j\in J'\right\}$ であって ${\textstyle \bigcup _{j\in J'}5B_{j}\supset \bigcup _{j\in J}B_{j}\supset E}$ となるものを選ぶことができる。従って、

$\lambda _{d}(E)\leq \lambda _{d}{\biggl (}\bigcup _{j\in J}B_{j}{\biggr )}\leq \lambda _{d}{\biggl (}\bigcup _{j\in J'}5B_{j}{\biggr )}\leq \sum _{j\in J'}\lambda _{d}(5B_{j}).$

ここで、d-次元球体の半径を5倍するとその体積は 5^d 倍されるので、

$\sum _{j\in J'}\lambda _{d}(5B_{j})=5^{d}\sum _{j\in J'}\lambda _{d}(B_{j})$

となり、

$\lambda _{d}(E)\leq 5^{d}\sum _{j\in J'}\lambda _{d}(B_{j}).$

となる。

ヴィタリの被覆定理

被覆定理においては、与えられた集合 E ⊆ R^d を E のヴィタリ被覆から取った互いに素な部分集合族によって高々"無視可能な集合"を残すまで覆いつくすことを目標とする。E の ヴィタリクラス または ヴィタリ被覆 ${\mathcal {V}}$ とは、それが集合の族であって、いかなる x ∈ E と δ > 0 についても、ある ${\mathcal {V}}$ の元 U を x ∈ U かつ U の直径が δ 未満の正の値となるように取れるもののことである。

ヴィタリによる古典的な設定では 無視可能な集合とはルベーグの意味で無視可能な集合、ルベーグ零集合のことである。しかし、以下の関連セクションで示されるように、ルベーグ測度以外の測度や R^d 以外の空間も今日までに考えられてきている。

次の観察は有用である: ${\mathcal {V}}$ が E のヴィタリ被覆であり E が開集合 Ω ⊆ R^d に含まれているとき、${\mathcal {V}}$ の元 U で Ω に含まれているもの全体はまた E のヴィタリ被覆である。

ルベーグ測度におけるヴィタリの被覆定理

次のルベーグ測度 λ_d についての被覆定理は Lebesgue (1910) によるものである。R^d の可測集合からなる族 ${\mathcal {V}}$ が(ルベーグの意味で) regular family であるとは、定数 C で次を満たすものが存在することである: ${\mathcal {V}}$ に属するいかなる集合 V に対しても

$\operatorname {diam} (V)^{d}\leq C\,\lambda _{d}(V)$.

立方体全てからなる族は regular family ${\mathcal {V}}$ の例である。R² の長方形で縦横比がある固定された m ≥ 1 についての m⁻¹ と m の間に収まるもの全体 ${\mathcal {V}}(m)$ なども例となる。R^d 上の任意のノルムが与えられているときのノルムに関連付けられた距離の球全体もまた例となる。これに対し、R² の長方形全ての族は regular ではない。

定理 ―  E ⊆ R^d を有限なルベーグ測度を持つ可測集合とし、let ${\mathcal {V}}$ を R^d の閉集合からなる regular family で E のヴィタリ被覆でもあるものとする。このとき、高々可算な互いに素な部分族 $\{U_{j}\}\subseteq {\mathcal {V}}$ で $$\lambda _{d}{\biggl (}E\setminus \bigcup _{j}U_{j}{\biggr )}=0.$$ となるものがとれる。

Vitali (1908) による元々の結果はこの定理の特別な場合である。それは d = 1 とし、${\mathcal {V}}$ が区間の集合であって、有限測度をもつ実数の部分集合 E のヴィタリ被覆となっている場合である.
上記定理は E が有限測度を持つことを仮定しなくとも成立する。というのも、各整数 n ≥ 0 について n < |x| < n+1 である点 x からなる開アニュラス Ω_n に含まれている E の断片それぞれについて有限測度に対する被覆の結果を適用すればよいからである。

多少関連する定理としてベシコビッチの被覆定理がある。A ⊆ R^d の各点 a に対して、中心 a 半径 r_a のユークリッド球体 B(a, r_a) が割り当てられているとする。このとき、ヴィタリの被覆定理でのように、これらの球体たちの部分族は特定の方法で A を被覆するために選ばれる。ベシコビッチの被覆定理とヴィタリの被覆補題の主な違いは、一つは、ヴィタリの非交和性の要求は次の条件に緩和される。任意の点 x ∈ R^d を含んでいる選ばれた球体の数 N_x は次元 d にのみ依存する定数 B_d によっておさえられるという条件である; もう一つは、選ばれた球体が与えられた中心全ての集合 A を覆うというものである。

ハウスドルフ測度に対するヴィタリの被覆定理

ルベーグ測度の代わりにハウスドルフ測度を考えるときにも似たようなオブジェクトを得ることができる。次の定理はそのような状況に適用できる。

定理 ―  H^s で s-次元ハウスドルフ測度を表すとする。E ⊆ R^d を H^s-可測集合とし、${\mathcal {V}}$ を閉集合からなる E のヴィタリ被覆だとする。このとき、(高々可算の)互いに素な部分集合族 $\{U_{j}\}\subseteq {\mathcal {V}}$ で $$H^{s}\left(E\setminus \bigcup _{j}U_{j}\right)=0$$ または $$\sum _{j}\operatorname {diam} (U_{j})^{s}=\infty .$$ を満たすものが存在する。

さらに、E が有限な s-次元ハウスドルフ測度を持つとき、どんな ε > 0 についても、部分集合族{U_j} を

$H^{s}(E)\leq \sum _{j}\mathrm {diam} (U_{j})^{s}+\varepsilon .$

となるように取れる。この定理は上で与えたルベーグの結果を導く。実際、s = d で R^d 上のハウスドルフ測度 H^s はd-次元ルベーグ測度の定数倍に一致する。もし、互いに素な族 $\{U_{j}\}$ が regular であって、有限なルベーグ測度の可測な領域 B に含まれているなら、

$\sum _{j}\operatorname {diam} (U_{j})^{d}\leq C\sum _{j}\lambda _{d}(U_{j})\leq C\,\lambda _{d}(B)<+\infty$

であり、前の定理の最初の仮定のにおける二つ目の可能性を除外するものである。それは E がルベーグの意味で無視可能な集合を残すまで、選ばれた互いに素な部分族によって被覆されることを導く。

被覆補題から被覆定理へ

被覆補題は次のヴィタリの被覆定理の基本形の証明における中間ステップで用いることができる。

定理 ― E を R^d の部分集合とし、閉球の集合族 F が E のヴィタリ被覆だとする。このとき、ある互いに素な部分族 G で E を高々ルベーグ零集合を残すまで被覆できる。

証明: 一般性を失うことなく、F の球はいずれも退化しておらず半径は 1 以下としてよい。被覆補題の無限バージョンにより、F の可算で互いに素なある部分族 $\mathbf {G}$ が存在して、任意の球 B ∈ F に対してある C ∈ G があって B ⊂ 5C となる。r > 0 を固定し、G のどの球にも属さず中心 0 の半径 r の開球 B(r) に属するような z ∈ E の集合を Z で表すことにする。全ての r で Z がルベーグ零集合であることを示せばよい。

$\mathbf {G} _{r}=\{C_{n}\}_{n}$ で G に属する球で B(r) と交わるもの全体からなる部分族を表す。$\mathbf {G} _{r}$ は高々可算であったことに注意する。z ∈ Z を固定する。各 N について z は閉集合 $K=\bigcup _{n\leq N}C_{n}$ には属していない。これは Z の定義により明らかである。しかしヴィタリ被覆の性質により、球 B ∈ F で z を含んでいてかつ、B(r) に含まれていて K と交わらないものが取れる。G の性質により、球 B はある球 $C_{i}\in \mathbf {G}$ と交わり $5C_{i}$ に含まれる。しかし K と B は交わらないため、i > N でなければならない。つまり、ある i > N について $z\in 5C_{i}$ であり、

$Z\subset \bigcup _{n>N}5C_{n}.$

これによって、全ての N について次の不等式

$\lambda _{d}(Z)\leq \sum _{n>N}\lambda _{d}(5C_{n})=5^{d}\sum _{n>N}\lambda _{d}(C_{n}).$

が成り立つ。しかし、$\mathbf {G} _{r}$ の球は B(r+2) に含まれていて、それらは互いに素なので

$\sum _{n}\lambda _{d}(C_{n})<\infty .$

である。そうすると、先ほどの不等式の最右辺は N が無限大に近づくにつれて 0 に収束するので、Z はルベーグ零集合でなければならない。

無限次元空間において

ヴィタリの被覆定理は無限次元空間の設定においては正しくない。この方向の最初の結果は1979年デイビッド・プライスによって与えられた: (無限次元の) 可分 ヒルベルト空間 H 上のガウス測度 γ が (H, Borel(H), γ) に対してヴィタリの被覆定理が成立しないように存在する。この結果は2003年に Jaroslav Tišer によって強められた: 実は、どんな(無限次元)可分ヒルベルト空間の上でも全ての無限次元ガウス測度に対して、ヴィタリの被覆定理は成り立たない。

関連項目

• ベシコビッチの被覆定理

参考文献

• Evans, Lawrence C.; Gariepy, Ronald F. (1992), Measure Theory and Fine Properties of Functions, Studies in Advanced Mathematics, Boca Raton, FL: CRC Press, pp. viii+268, ISBN 0-8493-7157-0, MR1158660, Zbl 0804.28001 
• Falconer, Kenneth J. (1986), The geometry of fractal sets, Cambridge Tracts in Mathematics, 85, Cambridge: Cambridge University Press, pp. xiv+162, ISBN 0-521-25694-1, MR867284, Zbl 0587.28004 
• Hazewinkel, Michiel, ed. (2001), “Vitali theorem”, Encyclopaedia of Mathematics, Springer, ISBN 978-1-55608-010-4, http://eom.springer.de/p/v096780.htm 
• Lebesgue, Henri (1910), “Sur l'intégration des fonctions discontinues”, Annales Scientifiques de l'École Normale Supérieure 27: 361–450, doi:10.24033/asens.624, JFM 41.0457.01, http://www.numdam.org/item?id=ASENS_1910_3_27__361_0 
• Natanson, I. P (1955), Theory of functions of a real variable, New York: Frederick Ungar Publishing Co., pp. 277, MR0067952, Zbl 0064.29102 
• Preiss, David (1979), “Gaussian measures and covering theorems”, Commentatione Mathematicae Universitatis Carolinae 20 (1): 95–99, ISSN 0010-2628, MR526149, Zbl 0386.28015 
• Stein, Elias M.; Shakarchi, Rami (2005), Real analysis. Measure theory, integration, and Hilbert spaces, Princeton Lectures in Analysis, III, Princeton, NJ: Princeton University Press, pp. xx+402, ISBN 0-691-11386-6, MR2129625, Zbl 1081.28001 
• Tišer, Jaroslav (2003), “Vitali covering theorem in Hilbert space”, Transactions of the American Mathematical Society 355 (8): 3277–3289 (electronic), doi:10.1090/S0002-9947-03-03296-3, MR1974687, Zbl 1042.28014 
• Vitali, Giuseppe (1908) [17 December 1907], “Sui gruppi di punti e sulle funzioni di variabili reali” (Italian), Atti dell'Accademia delle Scienze di Torino 43: 75–92, JFM 39.0101.05, https://archive.org/stream/attidellarealeac43real#page/228/mode/2up  (Title translation) "On groups of points and functions of real variables" is the paper containing the first proof of Vitali covering theorem.