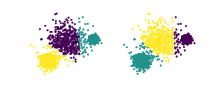 K平均法(左)および平均値シフト法(右)によるデータセットのクラスタリングの例。この2つのクラスタリングについて計算された調整ランド指数は
K平均法(左)および平均値シフト法(右)によるデータセットのクラスタリングの例。この2つのクラスタリングについて計算された調整ランド指数は 
ランド指数[1](ランドしすう、英: Rand index)またはランド測度(ランドそくど、英: Rand measure)は、統計、特にデータ・クラスタリングにおいて、2つのクラスタリングの類似性を図る尺度である。William M. Randにちなんで名付けられた。要素の偶然のグループ化を調整した形で定義したものが調整ランド指数である。数学的には、ランド指数は accuracy に関連しているが、クラスラベルを使用しない場合にも適用できる。
 個の要素からなる所与の集合
個の要素からなる所与の集合 および
および  の分割
の分割 および
および を考え、以下のように定義する。
を考え、以下のように定義する。
 は、
は、 の要素の組み合わせのうち、
の要素の組み合わせのうち、 で同じサブセット、
で同じサブセット、 で同じサブセットにあるものの数。
で同じサブセットにあるものの数。 は、
は、 の要素の組み合わせのうち、
の要素の組み合わせのうち、 で異なるサブセット、
で異なるサブセット、 で異なるサブセットにあるものの数。
で異なるサブセットにあるものの数。 は、
は、 の要素の組み合わせのうち、
の要素の組み合わせのうち、 で同じサブセット、
で同じサブセット、 で異なるサブセットにあるものの数。
で異なるサブセットにあるものの数。 は、
は、 の要素の組み合わせのうち、
の要素の組み合わせのうち、 で異なるサブセット、
で異なるサブセット、 で同じサブセットにあるものの数。
で同じサブセットにあるものの数。
ランド指数  は [1][2]
は [1][2]

直感的には、  は
は  と
と  の間の合意の数、
の間の合意の数、 は
は  と
と  の間の意見の相違の数と考えることができる 。
の間の意見の相違の数と考えることができる 。
分母はペアの総数なので、ランド指数はペアの総数に対する合意の発生頻度、つまり無作為に選ばれたペアにおいて  と
と  が合意する確率を表している。
が合意する確率を表している。
 は、
は、 として計算される。
として計算される。
同様に、次式のように、ランド指数 RI をアルゴリズムによる正しい判断の割合を示す指標として捉えることもできる。

- ここで、
 は真陽性の数、
は真陽性の数、 は真陰性の数、
は真陰性の数、  は偽陽性の数、
は偽陽性の数、 は偽陰性の数を表す。
は偽陰性の数を表す。
ランド指数は0〜1の値を持ち、0は2つのデータ・クラスタリングがどのペアでも一致しないことを、1はデータクラスタリングが全く同じであることを示す。
数学的には、a、b、c、dは次のように定義される。
 ,
, 
 ,
, 
 ,
, 
 ,
, 
(任意の に対して)
に対して)
ランドインデックスは、 の要素のペアを対象とした二項分類精度を通して見ることもできる。 2つのクラスラベルは「
の要素のペアを対象とした二項分類精度を通して見ることもできる。 2つのクラスラベルは「 と
と  が
が  と
と  の同じサブセットにある」 と「
の同じサブセットにある」 と「 と
と  が
が  と
と  の異なるサブセットにある」である。
の異なるサブセットにある」である。
その設定では、  は同じサブセットに属すると正しくラベル付けされたペアの数(真陽性)、
は同じサブセットに属すると正しくラベル付けされたペアの数(真陽性)、 は異なるサブセットに属すると正しくラベル付けされたペアの数(真陰性)である。
は異なるサブセットに属すると正しくラベル付けされたペアの数(真陰性)である。
調整ランド指数は、ランド指数を偶然性に基づいて補正したものである[1][2][3]。このような偶然性の補正は、ランダムに指定されたクラスタリング間のすべてのペアワイズ比較の類似度の期待値を使用して、ベースラインを確立します。従来、ランド指数は、クラスタリングのための順列モデル(クラスタリング内のクラスターの数とサイズは固定されており、すべてのランダムクラスタリングは、固定されたクラスター間で要素をシャッフルすることによって生成される)を用いて補正されていた。
しかし、順列モデルの前提は頻繁に破られる。多くのクラスタリングのシナリオでは、クラスターの数またはクラスターのサイズ分布が大幅に異なる。例えば、K平均法では、クラスターの数は実務者によって固定されているが、それらのクラスターのサイズはデータから推測されるものとする。調整ランド指数のバリエーションは、ランダムなクラスタリングのさまざまなモデルを説明する[4]。
ランド指数は0から1の間の値しか得られないが、調整ランド指数は、当てはまりが期待値よりも悪い場合、負の値を取り得る[5]。
 個の要素からなる集合
個の要素からなる集合  に対し、2つのグループ化または分割(クラスタリングなど)
に対し、2つのグループ化または分割(クラスタリングなど) と
と  を考える。
を考える。
 と
と  の重なりは、次のような分割表
の重なりは、次のような分割表 ![{\displaystyle \left[n_{ij}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf6d61cf9a2d775ae845160965e9e62ca6e038d3) にまとめることができる。ここで、
にまとめることができる。ここで、 のそれぞれは、
のそれぞれは、 と
と が共有するオブジェクトの数を表す 。すなわち、
が共有するオブジェクトの数を表す 。すなわち、 。
。

順列モデルを使用したオリジナルの調整ランド指数は
![{\displaystyle ARI={\frac {\left.\sum _{ij}{\binom {n_{ij}}{2}}-\left[\sum _{i}{\binom {a_{i}}{2}}\sum _{j}{\binom {b_{j}}{2}}\right]\right/{\binom {n}{2}}}{\left.{\frac {1}{2}}\left[\sum _{i}{\binom {a_{i}}{2}}+\sum _{j}{\binom {b_{j}}{2}}\right]-\left[\sum _{i}{\binom {a_{i}}{2}}\sum _{j}{\binom {b_{j}}{2}}\right]\right/{\binom {n}{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e0f6f21c547bd71629352a4b543119f6822d7ad)
ここで、 は分割表の値を表す。
は分割表の値を表す。
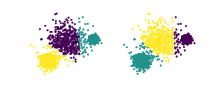





































![{\displaystyle \left[n_{ij}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf6d61cf9a2d775ae845160965e9e62ca6e038d3)





![{\displaystyle ARI={\frac {\left.\sum _{ij}{\binom {n_{ij}}{2}}-\left[\sum _{i}{\binom {a_{i}}{2}}\sum _{j}{\binom {b_{j}}{2}}\right]\right/{\binom {n}{2}}}{\left.{\frac {1}{2}}\left[\sum _{i}{\binom {a_{i}}{2}}+\sum _{j}{\binom {b_{j}}{2}}\right]-\left[\sum _{i}{\binom {a_{i}}{2}}\sum _{j}{\binom {b_{j}}{2}}\right]\right/{\binom {n}{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e0f6f21c547bd71629352a4b543119f6822d7ad)
