ドットアンドボックス
ドットアンドボックス (Dots and Boxes) は、2人(ときどきそれ以上)でペンと紙を用いて行うゲーム。19世紀にフランスの数学者エドゥアール・リュカにより最初に発表された。彼はこのゲームをla pipopipetteと呼んだ[1]。game of dots,[2] dot to dot grid,[3] boxes,[4] pigs in a pen[5]などさまざまな名前で呼ばれている[6]。
ルール
[編集]ゲームは点以外に何も書かれていないグリッドから始まる。
通常、2人のプレーヤーが繋がっていない隣接している2つの点の間に1本の水平線または垂直線を交互に加えていく。1×1のボックスの4番目の辺を引いたプレーヤーは1点を獲得し、次のターンも得る。線をこれ以上書けなくなるとゲームは終了し、最も多くの点を獲得したプレーヤーが勝者となる[6][7]。
グリッドの大きさには決まりはない。時間がない場合、またはゲームを学ぶときには2×2のボード(3×3の点)が適している[8]。5×5のボードはエキスパートに適している[9]。
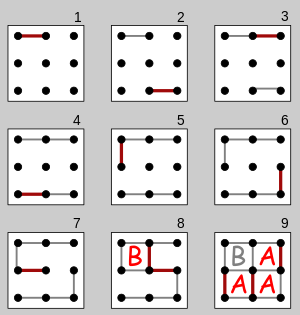
右図は2×2のボード(3×3の点)でプレーしたゲームが示されている。2番目のプレーヤー("B")は1番目のプレーヤー("A")の動きの回転鏡像の動きをし、ボードを2つに分割しゲームを引き分けんとする。しかしAは動作7で犠牲を払い、Bはその犠牲を受け入れ1つのボックスを獲得する。しかし、このときBはさらに1本線を加えなくてはならないため、中央の点と中央右の点を接続する。これにより残りの獲得されていないボックスが「チェーン」で結合される(動作8の最後)。Aは次の動作で3つのすべてのボックスを獲得し、3-1で勝利する。
戦略
[編集]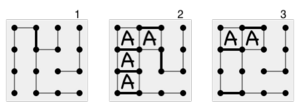
ほとんどの初心者のプレーヤーにとって、ゲームは点を多少ランダムに接続する段階から始まる。このときの唯一の戦略はボックスに3番目の辺を加えないことである。これは残り全ての(潜在的な)ボックスが「チェーン」(1つ以上の隣接するボックスのグループで、何らかの動作をするとチェーン内のすべてのボックスが相手に取られてしまう)につながるまで続く。この時点でプレーヤーは通常得られるすべてのボックスを手にし、得られる最小のチェーンを相手に渡す。例えば、右図の1に示すような状況に直面した初心者のプレーヤーはいくつかのボックスを取ることができるため、チェーンのすべてのボックスを獲得し2の状況に至る。しかし、最後の動作でより大きなチェーンを相手に渡さなくてはならず、最終的に負けてしまう[6][10]。
より熟練なプレーヤーは状況1に直面すると、代わりに「ダブルクロス戦略」を採用しチェーンのうち2つのボックスを除くボックスを取り、状況3で相手に渡す。相手はこれらの2つのボックスを取り、より大きいチェーンを作らなくてはならなくなる。状況3となればプレーヤーAは勝利となる。長いチェーンの数に関わらず同じダブルクロス戦略が適用される。この戦略を使用するプレーヤーは各チェーンで2つのボックスを除くすべてのボックスを獲得し、最後のチェーンですべてのボックスを獲得する。チェーンが十分長い場合、このプレーヤーが勝利する。
ダブルクロス戦略を使用するエキスパート間の次のレベルの戦略的複雑さは(許されている場合)「コントロール」に対する戦いである。エキスパートなプレーヤーは、最初の長いチェーンを渡した方が通常は負けるため、相手に最初の長いチェーンを作らせようとする[6][10]。犠牲の概念を理解していないプレーヤーに対して、エキスパートは正しい数の犠牲を払い、勝利を確実にするのに十分な長さの最初のチェーンを相手が渡すように促す。もし相手も犠牲を払った場合、エキスパートは以前のプレーで取ることができた犠牲の数をさらに処理する必要がある。
組合せゲーム理論では、ドットアンドボックスは不偏ゲームであり、多くの状況がスプレイグ・グランディの定理を用いて解析することができる。しかし、ほとんどの不偏ゲームにあるnormal play convention(最後に動作したプレーヤーが勝利する)が欠けているため、解析がかなり複雑になる[6][10]。
他のグリッドと変形
[編集]四角形のグリッドに限られず、三角形のグリッド、六角形のグリッドでもプレーすることができる[6]。
「ストリングアンドコイン」と呼ばれる双対グラフの形式がある。このゲームはストリング(辺)で結ばれたコイン(頂点)のネットワークでプレーされる。プレイヤーは順番にストリングを切る。切ったときにストリングが付いていないコインが残った場合、プレイヤーはコインをポケットに入れ、次のターンを行う。勝者は最も多くのコインをポケットに入れたプレイヤーである。ストリングアンドコインは任意のグラフでプレーすることができる[6]。
ポーランドでプレーされる変形の1つであるKropkiでは、プレイヤーがその境界線が完了するとすぐにいくつかの正方形の領域を主張することができる[11]。ドットアンドボックスの解析では、標準のものがアメリカンボードと呼ばれているのに対して外側の線がすでに引かれた状態で始まるものはスウェディッシュボードと呼ばれている。外側のうち左と下に線がすでに引かれた状態で始まる中間のものはアイスランディックボードと呼ばれる[12]。
Trxiltと呼ばれるゲームは、ドットアンドボックスのいくつかの要素とチェスのいくつかの要素を組み合わせている。
出典
[編集]- ^ Lucas, Édouard (1895), “La Pipopipette: nouveau jeu de combinaisons”, L'arithmétique amusante, Paris: Gauthier-Villars et fils, pp. 204–209.
- ^ Holladay, J. C. (1966), “A note on the game of dots”, American Mathematical Monthly 73: 717–720, doi:10.2307/2313978, MR0200068.
- ^ Swain, Heather (2012), Play These Games: 101 Delightful Diversions Using Everyday Items, Penguin, pp. 160–162, ISBN 9781101585030.
- ^ Solomon, Eric (1993), “Boxes: an enclosing game”, Games with Pencil and Paper, Dover Publications, Inc., pp. 37–39, ISBN 9780486278728. Reprint of 1973 publication by Thomas Nelson and Sons.
- ^ King, David C. (1999), Civil War Days: Discover the Past with Exciting Projects, Games, Activities, and Recipes, American Kids in History, 4, Wiley, pp. 29–30, ISBN 9780471246121.
- ^ a b c d e f g Berlekamp, Elwyn R.; Conway, John H.; Guy, Richard K. (1982), “Chapter 16: Dots-and-Boxes”, Winning Ways for your Mathematical Plays, Volume 2: Games in Particular, Academic Press, pp. 507–550.
- ^ Berlekamp, Elwyn (2000), The Dots-and-Boxes Game: Sophisticated Child's Play, AK Peters, Ltd, ISBN 1-56881-129-2.
- ^ Berlekamp, Conway & Guy (1982), "the 4-box game", pp. 513–514.
- ^ Berlekamp (2000), p. xi: [the 5×5 board] "is big enough to be quite challenging, and yet small enough to keep the game reasonably short".
- ^ a b c West, Julian (1996), “Championship-level play of dots-and-boxes”, in Nowakowski, Richard, Games of No Chance, Berkeley: MSRI Publications, pp. 79–84.
- ^ Grzegorzka, Jakub. “Dots - rules of the game”. zagram.org. 2017年11月27日閲覧。
- ^ Wilson, David, Dots-and-Boxes Analysis Results, University of Wisconsin 2016年4月7日閲覧。.
関連項目
[編集]- 『Wi-Fi対応 世界のだれでもアソビ大全』・『世界のアソビ大全51』 - ドットアンドボックスが収録されている。
外部リンク
[編集]- Barile, Margherita. "Dots and Boxes". mathworld.wolfram.com (英語).
- Ilan Vardi, Dots Strategies.
- Playable version at Pencil and Paper Games
