 関数 f(x) = log x の点 x = 1 における多項式 pn(x) = Σn
関数 f(x) = log x の点 x = 1 における多項式 pn(x) = Σn
k = 0 (x − 1)kf(k)(1)/k! による近似
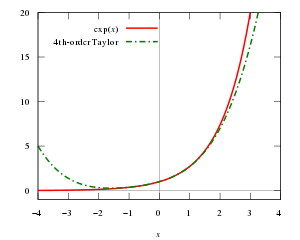 指数関数 y = ex(赤の実線)と原点のまわりでのその4次のテイラー多項式(緑の破線)。
指数関数 y = ex(赤の実線)と原点のまわりでのその4次のテイラー多項式(緑の破線)。
微分積分学において、テイラーの定理(テイラーのていり、英: Taylor's theorem)は、k 回微分可能な関数の与えられた点のまわりでの近似を k 次のテイラー多項式によって与える。解析関数に対しては、与えられた点におけるテイラー多項式は、そのテイラー級数を有限項で切ったものである。テイラー級数は関数を点のある近傍において完全に決定する。「テイラーの定理」の正確な内容は1つに定まっているわけではなくいくつかのバージョンがあり、状況に応じて使い分けられる。バージョンのいくつかは関数のテイラー多項式による近似誤差の明示的な評価を含んでいる。
テイラーの定理は1712年に1つのバージョンを述べた数学者ブルック・テイラー (Brook Taylor) にちなんで名づけられている。しかし誤差の明示的な表現はかなり後になってジョゼフ=ルイ・ラグランジュ (Joseph-Louis Lagrange) によってはじめて与えられた。結果の初期のバージョンはすでに1671年にジェームス・グレゴリー (James Gregory) によって言及されている[1]。
テイラーの定理は微分積分学の入門レベルで教えられ、解析学の中心的な初等的道具の1つである。純粋数学ではより進んだ漸近解析(英語版)の入り口であり、より応用的な分野の数値解析や数理物理学においてよく使われている。テイラーの定理は任意次元 n, m の多変数ベクトル値関数 f: Rn → Rm にも一般化する。テイラーの定理のこの一般化は微分幾何学や偏微分方程式において現れるいわゆるジェット(英語版)の定義の基礎である。
 | この節には内容がありません。 加筆して下さる協力者を求めています。 |
テイラーの定理の最も基本的なバージョンの正確なステートメントは次のようになる:
テイラーの定理[2][3][4] ― k ≥ 1 を整数とし関数 f: R → R を点 a ∈ R で k 回微分可能とする。すると次を満たす関数 hk: R → R が存在する:


これはペアノの剰余項と呼ばれる。
テイラーの定理に現れる多項式は関数 f の点 a における k 次のテイラー多項式

である。テイラー多項式は次のような意味で「漸近的に最もフィットする」唯一の多項式である、すなわち、関数 hk: R → R と k 次多項式 p が存在して

となるならば、p = Pk である。テイラーの定理は剰余項

の漸近的な振る舞いを記述する。これは f をテイラー多項式で近似するときの近似誤差である。ランダウの記号を用いれば、テイラーの定理のステートメントは次のように書ける:

f へのより強い正則性の仮定のもとで、テイラー多項式の剰余項

に対するいくつかの正確な公式がある。最も一般的なものたちは以下のものである。
平均値形の剰余項 ― f: R → R を閉区間 [a, x] 上 k 回連続微分可能、開区間 (a, x) 上 k + 1 (k ≥ 0) 回微分可能であるとする。 (x<a のときは区間をそれぞれ [x, a], (x, a) とする。) このとき

となる実数 ξL が a と x の間(両端は含まない)に存在する。これはラグランジュの剰余項[5]である。同様に、

となる実数 ξC が a と x の間に存在する。これはコーシーの剰余項[6]である。 とおくことにより、剰余項はそれぞれ次の形と同値である。
とおくことにより、剰余項はそれぞれ次の形と同値である。


テイラーの定理のこれらの改良は通常平均値の定理を用いて証明されるため、その名前がある。また他の同様の表示も見つけられる。例えば、G(t) が閉区間上連続、開区間上で微分可能で導関数の値が非0ならば、

となる数 ξ が存在する。このバージョンはラグランジュとコーシーの剰余項を特別な場合として含んでおり、以下でコーシーの平均値の定理を用いて証明される。
積分形の剰余のステートメントはこれまでのものより進んでおり完全な一般性にはルベーグ積分論の理解が要求される。しかしながら、f の (k + 1) 階微分が閉区間 [a, x] 上連続であるならば、リーマン積分の意味でも成り立つ。
積分形の剰余項[8] ― f(k) を a と x の間の閉区間上絶対連続とする。すると

これはベルヌーイの剰余とも呼ばれる。閉区間上の f(k) の絶対連続性により、導関数 f(k+1) は L1 関数として存在し、結果は微分積分学の基本定理と部分積分を用いた形式的な計算により証明できる。
テイラー近似に現れる項の剰余項の正確な公式があるよりはむしろそれを評価できることの方が実用上しばしば有用である。f が a を含む区間 I において (k + 1) 回連続微分可能とする。実定数 q, Q が存在して I 上

とする。このとき剰余項は x > a のとき不等式

を満たし[10]、x < a のときも同様の評価が成り立つ。これはラグランジュの剰余の単純な帰結である。とくに、ある r > 0 で区間 I = (a−r, a+r) 上

ならば、すべての x ∈ (a−r, a+r) に対して

である。第二の不等式は一様評価と呼ばれる。区間 (a−r, a+r) 上すべての x に対して一様に成り立つからである。
 ex(青)の x = 0 を中心とする次数 k = 1, ..., 7 のテイラー多項式 Pk(赤)による近似。
ex(青)の x = 0 を中心とする次数 k = 1, ..., 7 のテイラー多項式 Pk(赤)による近似。
関数 f(x) = ex を区間 [−1, 1] 上で誤差が 10−5 を超えないように近似したいとしよう。この例で我々は指数関数の次の性質しか知らないとしよう:

これらの性質から次のことが従う。すべての k に対して f(k)(x) = ex であり、とくに、f(k)(0) = 1 である。したがって f の 0 における k 次のテイラー多項式とそのラグランジュの剰余項は

によって与えられる、ただし ξ は 0 と x の間のある数である。ex は (*) によって増加関数だから、部分区間 [−1, 0] 上で剰余項を評価するのに単純に ex ≤ 1 (x ∈ [−1, 0]) を使うことができる。[0, 1] 上の剰余の上界を得るには、0<ξ<x に対して eξ<ex という性質を用いて、二次のテイラー展開を用いて

と評価できる。ex について解いて、単純に分子を最大化、分母を最小化して、

を得る。ex に対するこれらの評価を組み合わせて、

となるので、要求された正確さは

のときに確かに達成されている。(値 9! = 362 880 および 10! = 3 628 800 は階乗を参照するか手計算せよ。)結論として、テイラーの定理から次の近似が導かれる:

例えば、この近似から小数点以下五桁まで正しい小数表示  が得られる。
が得られる。
 | この節には内容がありません。 加筆して下さる協力者を求めています。 |
関数 f: Rn → R が a ∈ Rn において微分可能であることは、次と同値である。

となるような線型汎関数 L: Rn → R と関数 h: Rn → R が存在する。
この条件が成り立つとき、L = df(a) は点 a における f の(一意的に定義される)微分である。さらに、このとき f の a における偏微分が存在し、f の a における微分は

によって与えられる。
次のような多重指数表記を導入する。α ∈ Nn と x ∈ Rn に対して、

f: Rn → R のすべての k 階偏導関数が a ∈ Rn において連続ならば、クレローの定理より、a における混合微分の順序を入れ替えることができ、したがって高階偏導関数に対する表記

がこの状況において正当化される。f のすべての (k − 1) 階偏導関数が a のある近傍において存在し a において微分可能であれば、同じことが正しい[11]。このとき f は点 a において k 回微分可能であるという。
テイラーの定理の多変数版[12] ― f: Rn → R を点 a∈Rn において k 回微分可能な関数とする。このとき次を満たす hα: Rn→R が存在する:


関数 f: Rn → R が閉球 B において k + 1 回連続微分可能ならば、f の k + 1 階偏導関数を用いてこの近傍において剰余項の正確な公式を導出できる。すなわち、

このとき、コンパクト集合 B における k + 1 階偏導関数の連続性によって、ただちに次の一様評価を得る。

例えば、関数 f: R2 → R の三階のテイラー多項式は、x − a = v と書いて、

f は点 a ∈ R で k 回微分可能であることから a の適当な近傍で k-1 回微分可能である。この近傍の上で

と定める。ただし

ここで j = 0,1,...,k−1 に対し  であるから、ロピタルの定理を k−1 回適用すると
であるから、ロピタルの定理を k−1 回適用すると
![{\displaystyle {\begin{aligned}\lim _{x\to a}{\frac {f(x)-P_{k}(x)}{(x-a)^{k}}}&=\lim _{x\to a}{\frac {(d/dx)(f(x)-P_{k}(x))}{(d/dx)(x-a)^{k}}}=\cdots =\lim _{x\to a}{\frac {(d/dx)^{k-1}(f(x)-P_{k}(x))}{(d/dx)^{k-1}(x-a)^{k}}}\\&={\frac {1}{k!}}\lim _{x\to a}\left[{\frac {f^{(k-1)}(x)-f^{(k-1)}(a)}{x-a}}-f^{(k)}(a)\right]\\&={\frac {1}{k!}}(f^{(k)}(a)-f^{(k)}(a))=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f2740b27b1c8fc1fb4c05d9fe15412f4ebb2aa6)
ここで最後の等式は点 a での微分の定義による。従って

簡単のために a<x とする。まず任意の実関数 G で閉区間 [a, x] で連続、開区間 (a, x) で微分可能、さらに導関数 G' の値が開区間上で非0となるものを考える。
次に関数 F を

と定めると、 F は閉区間 [a, x] で連続、開区間 (a, x) で微分可能である。するとコーシーの平均値の定理により

を満たす点 ξ∈(a,x) が存在する。F の導関数を計算すると、

これを(*)に代入して計算すると

ここで  と定めればラグランジュの剰余項、
と定めればラグランジュの剰余項、  と定めればコーシーの剰余項が得られる。
と定めればコーシーの剰余項が得られる。
簡単のために a<x とする。まず f(k) が閉区間 [a, x] で絶対連続 であることから、その導関数 f(k+1) が L1-関数 の意味で存在する。ここで部分積分を繰り返し用いると
![{\displaystyle {\begin{aligned}f(x)&=f(a)+\int _{a}^{x}f'(t)\,dt\\&=f(a)-{\Big [}(x-t)f'(t){\Big ]}_{a}^{x}+\int _{a}^{x}(x-t)f''(t)\,dt\\&=f(a)+(x-a)f'(a)+\int _{a}^{x}(x-t)f''(t)\,dt\\&=f(a)+(x-a)f'(a)+{\frac {1}{2}}(x-a)^{2}f''(a)+\int _{a}^{x}{\frac {1}{2}}(x-t)^{2}f'''(t)\,dt\\&=\dots \\&=f(a)+{\frac {f'(a)}{1!}}(x-a)+\cdots +{\frac {f^{(k)}(a)}{k!}}(x-a)^{k}+\int _{a}^{x}{\frac {f^{(k+1)}(t)}{k!}}(x-t)^{k}\,dt\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08e0d9aa4d8dea863dffa9808e9dbef674178697)
最後の項  が求める剰余項である。
が求める剰余項である。
- ^ Kline 1972, pp. 442, 464
- ^ Genocchi, Angelo; Peano, Giuseppe (1884), Calcolo differenziale e principii di calcolo integrale, (N. 67, p.XVII-XIX): Fratelli Bocca ed.
- ^ Spivak, Michael (1994), Calculus (3rd ed.), Houston, TX: Publish or Perish, p. 383, ISBN 978-0-914098-89-8
- ^ Hazewinkel, Michiel, ed. (2001), “Taylor formula”, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Taylor_formula
- ^ Kline 1998, §20.3; Apostol 1967, §7.7.
- ^ Apostol 1967, §7.7.
- ^ Apostol 1967, §7.5.
- ^ Apostol 1967, §7.6
- ^ このことは、関数 f の偏導関数が a の近傍において存在し a において連続であるならば関数は a において微分可能であるという定理を繰り返し適用することによって従う。例えば次を参照。Apostol 1974, Theorem 12.11.
- ^ Königsberger Analysis 2, po. 64ff.
- ハイラー, E.、ヴァンナー, G. 著、蟹江幸博 訳『解析教程』 下、丸善出版、2012年。ISBN 978-4-621-06190-9。https://books.google.co.jp/books?id=zML3A8iCmeUC&pg=PA98。
- 杉浦, 光夫『解析入門I』東京大学出版会〈基礎数学2〉、1980年。ISBN 978-4-13-062005-5。
- Apostol, Tom (1967), Calculus, Wiley, ISBN 0-471-00005-1 .
- Apostol, Tom (1974), Mathematical analysis, Addison–Wesley .
- Bartle, Robert G.; Sherbert, Donald R. (2011), Introduction to Real Analysis (4th ed.), Wiley, ISBN 978-0-471-43331-6 .
- Hörmander, L. (1976), Linear Partial Differential Operators, Volume 1, Springer, ISBN 978-3-540-00662-6 .
- Kline, Morris (1972), Mathematical thought from ancient to modern times, Volume 2, Oxford University Press .
- Kline, Morris (1998), Calculus: An Intuitive and Physical Approach, Dover, ISBN 0-486-40453-6 .
- Pedrick, George (1994), A First Course in Analysis, Springer, ISBN 0-387-94108-8 .
- Stromberg, Karl (1981), Introduction to classical real analysis, Wadsworth, ISBN 978-0-534-98012-2 .
- Rudin, Walter (1987), Real and complex analysis (3rd ed.), McGraw-Hill, ISBN 0-07-054234-1 .










































![{\displaystyle {\begin{aligned}\lim _{x\to a}{\frac {f(x)-P_{k}(x)}{(x-a)^{k}}}&=\lim _{x\to a}{\frac {(d/dx)(f(x)-P_{k}(x))}{(d/dx)(x-a)^{k}}}=\cdots =\lim _{x\to a}{\frac {(d/dx)^{k-1}(f(x)-P_{k}(x))}{(d/dx)^{k-1}(x-a)^{k}}}\\&={\frac {1}{k!}}\lim _{x\to a}\left[{\frac {f^{(k-1)}(x)-f^{(k-1)}(a)}{x-a}}-f^{(k)}(a)\right]\\&={\frac {1}{k!}}(f^{(k)}(a)-f^{(k)}(a))=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f2740b27b1c8fc1fb4c05d9fe15412f4ebb2aa6)






![{\displaystyle {\begin{aligned}f(x)&=f(a)+\int _{a}^{x}f'(t)\,dt\\&=f(a)-{\Big [}(x-t)f'(t){\Big ]}_{a}^{x}+\int _{a}^{x}(x-t)f''(t)\,dt\\&=f(a)+(x-a)f'(a)+\int _{a}^{x}(x-t)f''(t)\,dt\\&=f(a)+(x-a)f'(a)+{\frac {1}{2}}(x-a)^{2}f''(a)+\int _{a}^{x}{\frac {1}{2}}(x-t)^{2}f'''(t)\,dt\\&=\dots \\&=f(a)+{\frac {f'(a)}{1!}}(x-a)+\cdots +{\frac {f^{(k)}(a)}{k!}}(x-a)^{k}+\int _{a}^{x}{\frac {f^{(k+1)}(t)}{k!}}(x-t)^{k}\,dt\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08e0d9aa4d8dea863dffa9808e9dbef674178697)
