コッドのセル・オートマトン
コッドのセル・オートマトン(Codd's cellular automaton)は、1968年、イギリス人計算機科学者エドガー・F・コッドが考案したセル・オートマトン (CA)。フォン・ノイマンのセル・オートマトンと同様の計算・構築万能性を有しているが、フォン・ノイマンのCAが29状態だったのに対して8状態で構成されている。コッドはそのCAで universal constructor のように自己複製機械を構成可能であることを示したが、2009年までそれが完全に実装されることはなかった。
歴史
[編集]1940年代から50年代にかけて、ジョン・フォン・ノイマンは以下のような問題を提示した[1]:
- 自身を複製するのに十分なオートマトンとはどのような論理構成か?
彼は29の状態を持つセル・オートマトンを構築し、それを使って universal constructor を生み出した。1968年、コッドはもっと単純な 8 状態だけからなるマシンを発見した[2]。したがってフォン・ノイマンの問題は次のように修正されなければならなくなった:
- 自身を複製するのに「必要十分な」オートマトンとはどのような論理構成か?
コッドのCAの発表から3年後、Edwin Roger Banks が博士論文で計算および構築の万能性を示す4状態のCAを提示した。ただし、コッドもBanksもそのCA上の自己複製機械の構成を示していない[3]。1973年、John Devore が修士論文でコッドのCAを改良して大幅に単純化し、当時のコンピュータ上で実装可能な規模にした。しかし、自己複製のためのデータテープは非常に長く、実際に自己複製が確認できたのは Golly というプログラムが開発されてからのことである。クリストファー・ラングトンは1984年、コッドのセル・オートマトンをさらに単純化したものを考案した。ラングトンのループと呼ばれ、はるかに少ないセル数で自己複製機能を実現しているが、計算と構築の万能性は失われている[4]。
各種CAの比較
[編集]| CA | 状態数 | 対称性 | 計算・構築万能性 | 自己複製機械の大きさ |
|---|---|---|---|---|
| フォン・ノイマン | 29 | なし | あり | 130,622セル |
| コッド | 8 | 回転対称 | あり | 283,126,588セル[5] |
| Devore | 8 | 回転対称 | あり | 94,794セル |
| Banks-IV | 4 | 回転および鏡像 | あり | 不明 |
| ラングトンのループ | 8 | 回転対称 | なし | 86セル |
仕様
[編集]
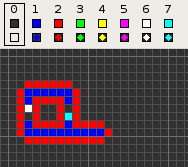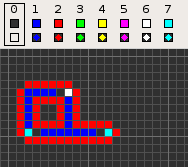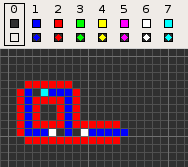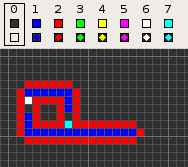
コッドのセル・オートマトンは回転対称性のある4近傍(フォン・ノイマン近傍)、8状態のセル・オートマトンである。そのコンセプトは空のフィールド(0)上の経路(1)に基づいている。経路は信号の通る導線であり、4から7の状態で構成され、後ろには 1 個の状態0のセルが置かれて転送の方向を定義している。信号が空のフィールド(状態0で満たされた空間)に漏れ出すのを防ぐため、経路の周囲は状態2の線で被覆されている。このような基本構成はその後の多くのセル・オートマトンでも採用されている。例えば、ワイヤワールドなどがある。
次の表は、様々な機能を持った信号列を示している。一部の信号列は導線内での衝突を防ぐため、少なくとも2セルの空白(状態1)で分離される必要がある。そのため本項目の冒頭にある動画は 'extend' の動作を示しているが、下の表ではそれを(最も短い) '70116011' としている。
| 用途 | 信号列 |
|---|---|
| extend | 70116011 |
| extend_left | 4011401150116011 |
| extend_right | 5011501140116011 |
| retract | 4011501160116011 |
| retract_left | 5011601160116011 |
| retract_right | 4011601160116011 |
| mark | 701160114011501170116011 |
| erase | 601170114011501160116011 |
| sense | 70117011 |
| cap | 40116011 |
| inject_sheath | 701150116011 |
| inject_trigger | 60117011701160116011 |
コンピュータの構築
[編集]コッドは、WangのWマシン (Wang B-machine) に基づいて、このセル・オートマトン上で自己複製するコンピュータを設計した。しかしそれは極めて巨大な設計となり、Tim Hutton が2009年に明確な構成で構築するまで実装されなかった[5]。その過程でHuttonはコッドの設計に若干の誤りがあることを発見した。
脚注
[編集]- ^ von Neumann, John (1966年). “Theory of Self-Reproducing Automata.”. www.walenz.org. 2008年1月5日時点のオリジナルよりアーカイブ。2012年1月28日閲覧。
- ^ Codd, Edgar F. (1968). Cellular Automata. Academic Press, New York
- ^ Banks, Edwin (1971). Information Processing and Transmission in Cellular Automata. PhD thesis, MIT, Department of Mechanical Engineering
- ^ Langton, C. G. (1984). “Self-Reproduction in Cellular Automata”. Physica D: Nonlinear Phenomena 10 (1-2): 135–144. doi:10.1016/0167-2789(84)90256-2.
- ^ a b Hutton, Tim J. (2010). “Codd's self-replicating computer”. Artificial Life 16 (2): 99–117. doi:10.1162/artl.2010.16.2.16200. PMID 20067401.
関連項目
[編集]外部リンク
[編集]- Rule Table Repository - コッドのCAの状態遷移規則が掲載されている。
- Golly - コッドのCAやライフゲームなど様々なCAをサポートしたソフトウェア
- CoddsDesign - コッドが設計した自己複製コンピュータの詳細など
