グーイの磁気天秤
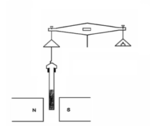
グーイの磁気天秤(グーイのじきてんびん)とは、ルイ・ジョルジュ・グーイが発明した、試料の磁化率を測る機器である。
背景
[編集]グーイは、ブラウン運動、実験物理学へ広い関心を持っていたが、中でも磁気的な現象に特に興味を持っていた。彼は1889年に一様磁場下の物質の相互作用は磁化率に比例するとする数式を導いた。この導出において、彼は試験管に磁場を印加し、そこに吊り下げられた試料にかかる力を天秤で計測することにより彼の式に表われる磁化率を計測する方法を提案した。彼は自身の科学的提案を検証することはなかったが、この単純で安価に実行できる方法は磁化率を計測する上で基礎的な方法となり、グーイの磁気天秤の原型となった[1]。
手順
[編集]グーイの磁気天秤は、強い磁場下におかれた試料の磁力によるみかけの質量変化を計測する[2]。市販されているものの一部には、このためのポートが基部に設けられている。使用時には、長い円筒状の試料を一部が磁石の磁極の間にはさまれるように天秤に吊す。試料は固体でも液体でもよく、試験管などの円筒状容器に入れることが多い。固体化合物試料は、一様になるように細粉状にするのが一般的である[3]。試料を磁極間に吊すのには付属する糸を用いる[2]。測定時には、二回に分けて値を読む必要がある。まず、磁場を印加するまえの読み (ma) を記録する。次に、磁場を印加した状態での読み (mb) を記録する。その差 (mb − ma) から試料に働いた磁力を求められる[2]。
考え方
[編集]磁場を印加する前後のみかけの質量差は、試料に働いた磁力の結果である。印加される磁場には場所によって強弱の勾配がある。常磁性の試料は磁石に向けて引っぱられ、みかけの質量差 mb − ma は正となる。反磁性の試料の場合は、磁場からの弱い斥力のためにみかけの質量差はゼロとなる場合も負となる場合もある[4]。常磁性の試料では誘導磁場は印加磁場よりも強くなり、磁化率は正となる。反磁性試料では誘導磁場は印加磁場よりもとても小さく、磁化率は負となる[5]。下の数式により、みかけの質量差から試料の磁化率を求めることができる。
F = (mb − ma)g = 1⁄2(K2 − K1)AH2 [3]
- mb − ma = みかけの質量差
- g = 重力加速度
- K1 = 試料の磁化率
- K2 = 媒質の磁化率(ほとんどの場合無視できる値)
- H = 印加磁場
- A = 試験管の断面積
機器
[編集]実用的な機器では、天秤および磁石全体はガラス箱の中に封入されており、気流による影響なく重量計測が行えるようになっている。異なる温度の試料について計測が行えるように、サーモスタットが組込まれていることもある[6]。グーイの磁気天秤には強い電磁石が必要なので、据置型の機器となる[2]。気流による影響を避けるため、気密を施した部屋の中の大理石の天秤台に据え付けることが多い[5]。グーイの磁気天秤に用いられる定常磁場は入り切りする必要があるので、通常は電磁石を用いて発生させる。
参照文献
[編集]- ^ Andrea Sella, "Gouy’s Tube", Royal Society of Chemistry, 2010
- ^ a b c d Saunderson, A. (1968). “A Permanent Magnet Gouy Balance”. Physics Education 3 (5): 272–273. Bibcode: 1968PhyEd...3..272S. doi:10.1088/0031-9120/3/5/007.
- ^ a b Brucacher, L.; Stafford, F. (1962). “Magnetic Susceptibility”. J. Chem. Educ. 39: 574. Bibcode: 1962JChEd..39..574B. doi:10.1021/ed039p574.
- ^ Neele Holzenkaempfer, Jesse Gipe "Magnetic Properties of Coordination Complexes", UCDavis ChemWiki
- ^ a b Liang, S.; Harrison, B.; Pagotto, J. (1997). “Determination of the Impregnant Concentrations on ASC Type Charcoal”. Defence Research Establishment Ottawa.
- ^ Earnshaw, Alan (1968). Introduction to Magnetochemistry. Academic Pressp. 89
