エトヴェシュの実験
この項目「エトヴェシュの実験」は翻訳されたばかりのものです。不自然あるいは曖昧な表現などが含まれる可能性があり、このままでは読みづらいかもしれません。(原文:英語版 04:58, 24 December 2018) 修正、加筆に協力し、現在の表現をより自然な表現にして下さる方を求めています。ノートページや履歴も参照してください。(2019年4月) |
エトヴェシュの実験(エトヴェシュのじっけん)は、慣性質量と重力質量の間の相関関係を測定した有名な物理学の実験であり、2つが同じものであることを実証した実験である。このことは長い間疑問に思われてはいたが、この実験と同じ正確さで実証されたことはそれまでなかった。最初期の実験はニュートンにより行われ、ベッセルにより改良された[1]。エトヴェシュによるトーションバランスを用いた実験は1882年ごろに始められ、1906年から1909年の長期にさらなる改良が加えられた。エトヴェシュのチームは、似ているがより精緻な実験を追試し、様々な材料で地球の様々な場所で実験を行った。これら全てにより同じ質量の等価性が実証された。続いて、これらの実験は一般相対論において符号化された、重力質量と慣性質量は同じであると述べる等価原理の現代的理解をもたらしている。
慣性質量は重力質量に比例していれば十分である。乗数定数は力の単位の定義に取り込まれる[2]。
エトヴェシュの元々の実験
[編集]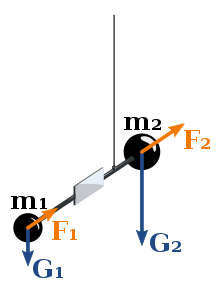

エトヴェシュの元々の実験装置は、棒の両端に2つの質量を取り付け、それを細い繊維でつりさげていた。棒、繊維に取り付けられた鏡が光を小さな望遠鏡に対して反射していた。棒の回転のわずかな変化でも光ビームが偏向され、望遠鏡で拡大するとそれが大きな変化にみえる。
地球の基準系(慣性座標系ではない「実験室系」)からわかるように、均衡質量に作用する主な力は張力、重力、地球の回転による遠心力である。重力はニュートンの万有引力の法則により計算され、これは重力質量に依存する。遠心力はニュートンの運動の法則により計算され、これは慣性質量に依存する。
この実験は2つのタイプの質量が異なる場合、2つの力が2つの物体に全く同じようには作用せず、時間がたつにつれて棒が回転するように準備された。回転する「実験室系」から見ると、弦の張力と(はるかに小さいが)遠心力の和が重力を相殺する(ベクトルとして)。慣性系から見ると常に重力と張力の(ベクトル)和が地球とともに物体を回転させる。
実験室系において棒を静止させるためには、棒に作用するそれぞれの物体に作用する張力の反作用が正味0のトルクを生み出す必要がある(唯一の自由度は水平面上での回転である)。系が絶えず静止していると仮定すると – これは力学的平衡を意味する(すなわち正味の力とトルクが0) – 吊り下げられた2つの物体は静止するが、系が静止しているという仮定に反して異なる遠心力が働くと結果として張力の反作用を通じて棒に異なるトルクが及び、棒が自然と回転する。そのため、系はこの状態では存在できない。2つの物体にかかる遠心力に差があると、棒が回転する。
さらなる改善
[編集]最初の実験は1885年頃に行われ、明白な違いがないことが実証され、エトヴェシュはこれをより正確に実証するために実験の改善を行った。1889年、材料による重力の変化があるかどうかを確かめるために異なるタイプの試料材料と装置を用いた。この実験では2000万分の1の要求精度でこの変化を測定できないことが証明された。1890年、ブダペストのゲッレールト山での質量測定とともにこれらの結果を発表した。[3]
翌年、自身で「水平バリオメータ」と呼んだ改良版の装置の研究を開始した。この改良版では基本的な設計をわずかに変更し、端に直接取り付けるのではなく2つの静止質量のうち1つを端から紐で吊るすようにした。これによりトーションを2次元において、さらにgの局所水平成分を測定することができた。ずっと正確なものでもあった。現在これは一般的にエトヴェシュの天秤(Eötvös balance)と呼ばれているが、今日でも局所的な質量集中の探索に広く使われている。
この新しい装置を用いた4000時間かけた一連の実験が、Dezsö Pekár (1873–1953) とJenő Fekete (1880–1943) により1906年に始められた。これは1909年にロンドンで開催された第16回国際測地線会議で初めて発表され、1億分の1の精度まで向上した[3]。エトヴェシュは1919年に亡くなり、完全な測定値は1922年にPekárとFeketeにより発表されたのみである。
関連する研究
[編集]エトヴェシュは他のチームにより動いている船で行われていた同様の実験も研究し、それが彼らが測定した小さな違いを説明するためのエトヴェシュ効果の発展につながった。これらは地球との関係における船の動きによる付加的な加速力によるものであり、この効果は1908年に黒海で行われた追加の航行で実証された。
1930年代、エトヴェシュの元生徒であるJános Renner (1889–1976)は結果を20億-50億分の1まで改善した[4]。ロバート・K・ディッケはP. G. RollとR. Krotkovとともに改良された装置を用いてずっと後に実験を再実行し、さらに精度を1000億分の1まで改善した[5]。また、彼らは主張された精度が幾分疑わしいことを示唆する最初の実験についてのいくつかの観察を行った。これらの懸念に照らしてのデータの再検討したところ、等価原理が厳密ではなく異なる種類の材料により変化したことを示唆するように思われるはっきりとしたわずかな効果につながった。
1980年代、重力と量子力学を組み合わせようとするいくつかの新たな物理理論は、物質と反物質が重力によりわずかに異なる影響を受けることを示唆した。Dickeの主張と組み合わせるとそのような違いが測定できる可能性があるように思われ、このことは新たなエトヴェシュ型の一連の実験につながった。最終的にそのような影響は示されなかった[6][7][8][9][10][11]。
これらの実験の副次的な影響は、局所層序の詳しい研究、物理学研究所の物理的設計(エトヴェシュが個人的に設計したもの)や天候やその他の影響までも含む最初のエトヴェシュのデータの再調査であった。したがって実験はよく記録されている[12]。
脚注
[編集]- ^ Marco Mamone Capria (2005). Physics Before and After Einstein. Amsterdam: IOS Press. p. 167. ISBN 1-58603-462-6
- ^ Brewer, Jess H. (1998年). “The Eötvös Experiment”. 2019年4月閲覧。
- ^ a b R. v.
- ^ J. Renner, Matematikai és Természettudományi Értesítő, 13, 542, 1935, with abstract in German
- ^ P. G. Roll, R. Krotkov, R. H. Dicke, Annals of Physics, 26, 442, 1964.
- ^ E.Fischbach, D. Sudarsky, A. Szafer, C. Talmadge, and S. H. Aronson, Reanalysis of the Eötvös Experiment, Phys.
- ^ H. H. Thodberg, Comment on the Sign in the Reanalysis of the Eötvös Experiment, Phys.
- ^ S. Y. Chu and R. H. Dicke, New Force or Thermal Gradient in the Eötvös Experiment?, Phys.
- ^ P. Vecsernyés, Constraints on a vector coupling to baryon number from the Eötvös experiment, Phys.
- ^ K. Nordtvedt, Lunar laser ranging and laboratory Eötvös-type experiments, Phys.
- ^ Wm. R. Bennett, Jr., Modulated-Source Eötvös Experiment at Little Goose Lock, Phys.
- ^ One Hundred Years of the Eötvös Experiment (archived from the original Archived October 22, 2012, at the Wayback Machine.
