アヤメの花データセット
アヤメの花データセット(アヤメのはなデータセット、英語: Iris flower data set)あるいはフィッシャーのアヤメデータセット(英語: Fisher's Iris data set)は1936年にイギリスの統計学者・生物学者ロナルド・フィッシャーが1936年の論文『The use of multiple measurements in taxonomic problems』で線形判別分析の例として用いた多変数データセットである[1]。エドガー・アンダーソンが3種の近縁なアヤメの形態変異を定量化するために記録したものであることから、アンダーソンのアヤメデータセット(英語: Anderson's Iris data set)とも呼ばれる[2]。3種のうち2つはガスペ半島の「同じ牧場で、同じ日に、同一人物によって同じ測定器で同時に」記録された[3]。
データセットはアヤメ3種(ヒオウギアヤメ、バージニアアヤメ、ヘンショクアヤメ)それぞれ50花ずつの標本からなる。各標本ごとに4つの特徴量(萼と花弁それぞれの長さと幅)がセンチメートル単位で測定されている。これら4つの特徴量の組み合わせから、フィッシャーはそれぞれの種を区別するための線形判別分析モデルを発達させた。フィッシャーの論文は『優生学会誌』(英語: Annals of Eugenics, 今日の『人間遺伝学会誌』)に掲載された[1]。
データセットの使用
[編集]

元々はフィッシャーの線形判別分析に用いられたが、その後サポートベクターマシンなどのような機械学習の分類のテストに用いられるようになった[5]。
しかしながら2つの明瞭に異なるクラスタのみが含まれることから、クラスタ解析ではあまり使用されない。ひとつのクラスタにはヒオウギアヤメが含まれ、もう片方のクラスタにはバージニアアヤメとヘンショクアヤメ両方が含まれており、両種はフィッシャーの用いた種情報なしでは判別不可能である。そのため、データマイニングの教師あり学習と教師なし学習の違いを説明する良い例となっている。すなわち、フィッシャーの線形判別モデルは対象種が明らかな場合のみ得られる。分類とクラスタは必ずしも一致しない[6]。
それにもかかわらず、3種のアヤメはどれも非線形で枝分かれする主成分分析によって判別できる[7]。データセットはノードの数が多すぎたり、曲げたり伸ばしたりすることに対して何らかのペナルティを課すことで、最も近いツリーによって近似され、いわゆる「地下鉄路線図」が構築される[4]。各ノードについて、投影された点の円グラフが作成される。円グラフの面積は投影点の数に比例する。左図から明らかなように、異なる種のアヤメのサンプルの絶対多数は、異なるノードに属している。バージニアアヤメのごく一部がヘンショクアヤメと混在しているだけである(図中の青緑色の混在ノード)。したがって、3種のアヤメ(ヒオウギアヤメ、バージニアアヤメ、ヘンショクアヤ)は、主成分ツリーの対応するノードを選ぶことで、非線形主成分分析の教師なし手順によって判別できる。
データセット
[編集]
データセットには150の記録が5指標下(萼と花弁それぞれの長さと幅、および種情報)で含まれる。



| 番号 | 萼幅 | 萼長 | 花弁幅 | 花弁長 | 種 |
|---|---|---|---|---|---|
| 1 | 5.1 | 3.5 | 1.4 | 0.2 | ヒオウギアヤメ |
| 2 | 4.9 | 3.0 | 1.4 | 0.2 | ヒオウギアヤメ |
| 3 | 4.7 | 3.2 | 1.3 | 0.2 | ヒオウギアヤメ |
| 4 | 4.6 | 3.1 | 1.5 | 0.2 | ヒオウギアヤメ |
| 5 | 5.0 | 3.6 | 1.4 | 0.3 | ヒオウギアヤメ |
| 6 | 5.4 | 3.9 | 1.7 | 0.4 | ヒオウギアヤメ |
| 7 | 4.6 | 3.4 | 1.4 | 0.3 | ヒオウギアヤメ |
| 8 | 5.0 | 3.4 | 1.5 | 0.2 | ヒオウギアヤメ |
| 9 | 4.4 | 2.9 | 1.4 | 0.2 | ヒオウギアヤメ |
| 10 | 4.9 | 3.1 | 1.5 | 0.1 | ヒオウギアヤメ |
| 11 | 5.4 | 3.7 | 1.5 | 0.2 | ヒオウギアヤメ |
| 12 | 4.8 | 3.4 | 1.6 | 0.2 | ヒオウギアヤメ |
| 13 | 4.8 | 3.0 | 1.4 | 0.1 | ヒオウギアヤメ |
| 14 | 4.3 | 3.0 | 1.1 | 0.1 | ヒオウギアヤメ |
| 15 | 5.8 | 4.0 | 1.2 | 0.2 | ヒオウギアヤメ |
| 16 | 5.7 | 4.4 | 1.5 | 0.4 | ヒオウギアヤメ |
| 17 | 5.4 | 3.9 | 1.3 | 0.4 | ヒオウギアヤメ |
| 18 | 5.1 | 3.5 | 1.4 | 0.3 | ヒオウギアヤメ |
| 19 | 5.7 | 3.8 | 1.7 | 0.3 | ヒオウギアヤメ |
| 20 | 5.1 | 3.8 | 1.5 | 0.3 | ヒオウギアヤメ |
| 21 | 5.4 | 3.4 | 1.7 | 0.2 | ヒオウギアヤメ |
| 22 | 5.1 | 3.7 | 1.5 | 0.4 | ヒオウギアヤメ |
| 23 | 4.6 | 3.6 | 1.0 | 0.2 | ヒオウギアヤメ |
| 24 | 5.1 | 3.3 | 1.7 | 0.5 | ヒオウギアヤメ |
| 25 | 4.8 | 3.4 | 1.9 | 0.2 | ヒオウギアヤメ |
| 26 | 5.0 | 3.0 | 1.6 | 0.2 | ヒオウギアヤメ |
| 27 | 5.0 | 3.4 | 1.6 | 0.4 | ヒオウギアヤメ |
| 28 | 5.2 | 3.5 | 1.5 | 0.2 | ヒオウギアヤメ |
| 29 | 5.2 | 3.4 | 1.4 | 0.2 | ヒオウギアヤメ |
| 30 | 4.7 | 3.2 | 1.6 | 0.2 | ヒオウギアヤメ |
| 31 | 4.8 | 3.1 | 1.6 | 0.2 | ヒオウギアヤメ |
| 32 | 5.4 | 3.4 | 1.5 | 0.4 | ヒオウギアヤメ |
| 33 | 5.2 | 4.1 | 1.5 | 0.1 | ヒオウギアヤメ |
| 34 | 5.5 | 4.2 | 1.4 | 0.2 | ヒオウギアヤメ |
| 35 | 4.9 | 3.1 | 1.5 | 0.2 | ヒオウギアヤメ |
| 36 | 5.0 | 3.2 | 1.2 | 0.2 | ヒオウギアヤメ |
| 37 | 5.5 | 3.5 | 1.3 | 0.2 | ヒオウギアヤメ |
| 38 | 4.9 | 3.6 | 1.4 | 0.1 | ヒオウギアヤメ |
| 39 | 4.4 | 3.0 | 1.3 | 0.2 | ヒオウギアヤメ |
| 40 | 5.1 | 3.4 | 1.5 | 0.2 | ヒオウギアヤメ |
| 41 | 5.0 | 3.5 | 1.3 | 0.3 | ヒオウギアヤメ |
| 42 | 4.5 | 2.3 | 1.3 | 0.3 | ヒオウギアヤメ |
| 43 | 4.4 | 3.2 | 1.3 | 0.2 | ヒオウギアヤメ |
| 44 | 5.0 | 3.5 | 1.6 | 0.6 | ヒオウギアヤメ |
| 45 | 5.1 | 3.8 | 1.9 | 0.4 | ヒオウギアヤメ |
| 46 | 4.8 | 3.0 | 1.4 | 0.3 | ヒオウギアヤメ |
| 47 | 5.1 | 3.8 | 1.6 | 0.2 | ヒオウギアヤメ |
| 48 | 4.6 | 3.2 | 1.4 | 0.2 | ヒオウギアヤメ |
| 49 | 5.3 | 3.7 | 1.5 | 0.2 | ヒオウギアヤメ |
| 50 | 5.0 | 3.3 | 1.4 | 0.2 | ヒオウギアヤメ |
| 51 | 7.0 | 3.2 | 4.7 | 1.4 | ヘンショクアヤメ |
| 52 | 6.4 | 3.2 | 4.5 | 1.5 | ヘンショクアヤメ |
| 53 | 6.9 | 3.1 | 4.9 | 1.5 | ヘンショクアヤメ |
| 54 | 5.5 | 2.3 | 4.0 | 1.3 | ヘンショクアヤメ |
| 55 | 6.5 | 2.8 | 4.6 | 1.5 | ヘンショクアヤメ |
| 56 | 5.7 | 2.8 | 4.5 | 1.3 | ヘンショクアヤメ |
| 57 | 6.3 | 3.3 | 4.7 | 1.6 | ヘンショクアヤメ |
| 58 | 4.9 | 2.4 | 3.3 | 1.0 | ヘンショクアヤメ |
| 59 | 6.6 | 2.9 | 4.6 | 1.3 | ヘンショクアヤメ |
| 60 | 5.2 | 2.7 | 3.9 | 1.4 | ヘンショクアヤメ |
| 61 | 5.0 | 2.0 | 3.5 | 1.0 | ヘンショクアヤメ |
| 62 | 5.9 | 3.0 | 4.2 | 1.5 | ヘンショクアヤメ |
| 63 | 6.0 | 2.2 | 4.0 | 1.0 | ヘンショクアヤメ |
| 64 | 6.1 | 2.9 | 4.7 | 1.4 | ヘンショクアヤメ |
| 65 | 5.6 | 2.9 | 3.6 | 1.3 | ヘンショクアヤメ |
| 66 | 6.7 | 3.1 | 4.4 | 1.4 | ヘンショクアヤメ |
| 67 | 5.6 | 3.0 | 4.5 | 1.5 | ヘンショクアヤメ |
| 68 | 5.8 | 2.7 | 4.1 | 1.0 | ヘンショクアヤメ |
| 69 | 6.2 | 2.2 | 4.5 | 1.5 | ヘンショクアヤメ |
| 70 | 5.6 | 2.5 | 3.9 | 1.1 | ヘンショクアヤメ |
| 71 | 5.9 | 3.2 | 4.8 | 1.8 | ヘンショクアヤメ |
| 72 | 6.1 | 2.8 | 4.0 | 1.3 | ヘンショクアヤメ |
| 73 | 6.3 | 2.5 | 4.9 | 1.5 | ヘンショクアヤメ |
| 74 | 6.1 | 2.8 | 4.7 | 1.2 | ヘンショクアヤメ |
| 75 | 6.4 | 2.9 | 4.3 | 1.3 | ヘンショクアヤメ |
| 76 | 6.6 | 3.0 | 4.4 | 1.4 | ヘンショクアヤメ |
| 77 | 6.8 | 2.8 | 4.8 | 1.4 | ヘンショクアヤメ |
| 78 | 6.7 | 3.0 | 5.0 | 1.7 | ヘンショクアヤメ |
| 79 | 6.0 | 2.9 | 4.5 | 1.5 | ヘンショクアヤメ |
| 80 | 5.7 | 2.6 | 3.5 | 1.0 | ヘンショクアヤメ |
| 81 | 5.5 | 2.4 | 3.8 | 1.1 | ヘンショクアヤメ |
| 82 | 5.5 | 2.4 | 3.7 | 1.0 | ヘンショクアヤメ |
| 83 | 5.8 | 2.7 | 3.9 | 1.2 | ヘンショクアヤメ |
| 84 | 6.0 | 2.7 | 5.1 | 1.6 | ヘンショクアヤメ |
| 85 | 5.4 | 3.0 | 4.5 | 1.5 | ヘンショクアヤメ |
| 86 | 6.0 | 3.4 | 4.5 | 1.6 | ヘンショクアヤメ |
| 87 | 6.7 | 3.1 | 4.7 | 1.5 | ヘンショクアヤメ |
| 88 | 6.3 | 2.3 | 4.4 | 1.3 | ヘンショクアヤメ |
| 89 | 5.6 | 3.0 | 4.1 | 1.3 | ヘンショクアヤメ |
| 90 | 5.5 | 2.5 | 4.0 | 1.3 | ヘンショクアヤメ |
| 91 | 5.5 | 2.6 | 4.4 | 1.2 | ヘンショクアヤメ |
| 92 | 6.1 | 3.0 | 4.6 | 1.4 | ヘンショクアヤメ |
| 93 | 5.8 | 2.6 | 4.0 | 1.2 | ヘンショクアヤメ |
| 94 | 5.0 | 2.3 | 3.3 | 1.0 | ヘンショクアヤメ |
| 95 | 5.6 | 2.7 | 4.2 | 1.3 | ヘンショクアヤメ |
| 96 | 5.7 | 3.0 | 4.2 | 1.2 | ヘンショクアヤメ |
| 97 | 5.7 | 2.9 | 4.2 | 1.3 | ヘンショクアヤメ |
| 98 | 6.2 | 2.9 | 4.3 | 1.3 | ヘンショクアヤメ |
| 99 | 5.1 | 2.5 | 3.0 | 1.1 | ヘンショクアヤメ |
| 100 | 5.7 | 2.8 | 4.1 | 1.3 | ヘンショクアヤメ |
| 101 | 6.3 | 3.3 | 6.0 | 2.5 | バージニアアヤメ |
| 102 | 5.8 | 2.7 | 5.1 | 1.9 | バージニアアヤメ |
| 103 | 7.1 | 3.0 | 5.9 | 2.1 | バージニアアヤメ |
| 104 | 6.3 | 2.9 | 5.6 | 1.8 | バージニアアヤメ |
| 105 | 6.5 | 3.0 | 5.8 | 2.2 | バージニアアヤメ |
| 106 | 7.6 | 3.0 | 6.6 | 2.1 | バージニアアヤメ |
| 107 | 4.9 | 2.5 | 4.5 | 1.7 | バージニアアヤメ |
| 108 | 7.3 | 2.9 | 6.3 | 1.8 | バージニアアヤメ |
| 109 | 6.7 | 2.5 | 5.8 | 1.8 | バージニアアヤメ |
| 110 | 7.2 | 3.6 | 6.1 | 2.5 | バージニアアヤメ |
| 111 | 6.5 | 3.2 | 5.1 | 2.0 | バージニアアヤメ |
| 112 | 6.4 | 2.7 | 5.3 | 1.9 | バージニアアヤメ |
| 113 | 6.8 | 3.0 | 5.5 | 2.1 | バージニアアヤメ |
| 114 | 5.7 | 2.5 | 5.0 | 2.0 | バージニアアヤメ |
| 115 | 5.8 | 2.8 | 5.1 | 2.4 | バージニアアヤメ |
| 116 | 6.4 | 3.2 | 5.3 | 2.3 | バージニアアヤメ |
| 117 | 6.5 | 3.0 | 5.5 | 1.8 | バージニアアヤメ |
| 118 | 7.7 | 3.8 | 6.7 | 2.2 | バージニアアヤメ |
| 119 | 7.7 | 2.6 | 6.9 | 2.3 | バージニアアヤメ |
| 120 | 6.0 | 2.2 | 5.0 | 1.5 | バージニアアヤメ |
| 121 | 6.9 | 3.2 | 5.7 | 2.3 | バージニアアヤメ |
| 122 | 5.6 | 2.8 | 4.9 | 2.0 | バージニアアヤメ |
| 123 | 7.7 | 2.8 | 6.7 | 2.0 | バージニアアヤメ |
| 124 | 6.3 | 2.7 | 4.9 | 1.8 | バージニアアヤメ |
| 125 | 6.7 | 3.3 | 5.7 | 2.1 | バージニアアヤメ |
| 126 | 7.2 | 3.2 | 6.0 | 1.8 | バージニアアヤメ |
| 127 | 6.2 | 2.8 | 4.8 | 1.8 | バージニアアヤメ |
| 128 | 6.1 | 3.0 | 4.9 | 1.8 | バージニアアヤメ |
| 129 | 6.4 | 2.8 | 5.6 | 2.1 | バージニアアヤメ |
| 130 | 7.2 | 3.0 | 5.8 | 1.6 | バージニアアヤメ |
| 131 | 7.4 | 2.8 | 6.1 | 1.9 | バージニアアヤメ |
| 132 | 7.9 | 3.8 | 6.4 | 2.0 | バージニアアヤメ |
| 133 | 6.4 | 2.8 | 5.6 | 2.2 | バージニアアヤメ |
| 134 | 6.3 | 2.8 | 5.1 | 1.5 | バージニアアヤメ |
| 135 | 6.1 | 2.6 | 5.6 | 1.4 | バージニアアヤメ |
| 136 | 7.7 | 3.0 | 6.1 | 2.3 | バージニアアヤメ |
| 137 | 6.3 | 3.4 | 5.6 | 2.4 | バージニアアヤメ |
| 138 | 6.4 | 3.1 | 5.5 | 1.8 | バージニアアヤメ |
| 139 | 6.0 | 3.0 | 4.8 | 1.8 | バージニアアヤメ |
| 140 | 6.9 | 3.1 | 5.4 | 2.1 | バージニアアヤメ |
| 141 | 6.7 | 3.1 | 5.6 | 2.4 | バージニアアヤメ |
| 142 | 6.9 | 3.1 | 5.1 | 2.3 | バージニアアヤメ |
| 143 | 5.8 | 2.7 | 5.1 | 1.9 | バージニアアヤメ |
| 144 | 6.8 | 3.2 | 5.9 | 2.3 | バージニアアヤメ |
| 145 | 6.7 | 3.3 | 5.7 | 2.5 | バージニアアヤメ |
| 146 | 6.7 | 3.0 | 5.2 | 2.3 | バージニアアヤメ |
| 147 | 6.3 | 2.5 | 5.0 | 1.9 | バージニアアヤメ |
| 148 | 6.5 | 3.0 | 5.2 | 2.0 | バージニアアヤメ |
| 149 | 6.2 | 3.4 | 5.4 | 2.3 | バージニアアヤメ |
| 150 | 5.9 | 3.0 | 5.1 | 1.8 | バージニアアヤメ |
アヤメデータセットは機械学習の初心者向けデータセットとして広く利用されている。R言語の基本パッケージやPythonのscikit-learnに含まれており、利用者が情報源を見つけることなく利用できる。
いくつかのバージョンが公表されている。
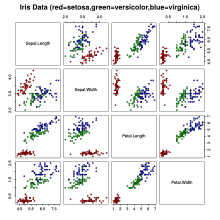
下に示すRコードによって当記事冒頭に示した散布図を再現できる。
# Show the dataset
iris
# Show the help page, with information about the dataset
?iris
# Create scatterplots of all pairwise combination of the 4 variables in the dataset
pairs(iris[1:4], main="Iris Data (red=setosa,green=versicolor,blue=virginica)",
pch=21, bg=c("red","green3","blue")[unclass(iris$Species)])
from sklearn.datasets import load_iris
iris = load_iris()
iris
次の結果が得られる。
{'data': array([[5.1, 3.5, 1.4, 0.2],
[4.9, 3., 1.4, 0.2],
[4.7, 3.2, 1.3, 0.2],
[4.6, 3.1, 1.5, 0.2],...
'target': array([0, 0, 0, ... 1, 1, 1, ... 2, 2, 2, ...
'target_names': array(['setosa', 'versicolor', 'virginica'], dtype='<U10'),
...}
関連項目
[編集]出典
[編集]- ^ a b R. A. Fisher (1936). “The use of multiple measurements in taxonomic problems”. Annals of Eugenics 7 (2): 179–188. doi:10.1111/j.1469-1809.1936.tb02137.x. hdl:2440/15227.
- ^ Edgar Anderson (1936). “The species problem in Iris”. Annals of the Missouri Botanical Garden 23 (3): 457–509. doi:10.2307/2394164. JSTOR 2394164.
- ^ Edgar Anderson (1935). “The irises of the Gaspé Peninsula”. Bulletin of the American Iris Society 59: 2–5.
- ^ a b Gorban, A. N.; Zinovyev, A. (2010). “Principal manifolds and graphs in practice: from molecular biology to dynamical systems”. International Journal of Neural Systems 20 (3): 219–232.
- ^ “UCI Machine Learning Repository: Iris Data Set”. archive.ics.uci.edu. 2017年12月1日閲覧。
- ^ Ines Färber; Stephan Günnemann; Hans-Peter Kriegel; Peer Kröger; Emmanuel Müller; Erich Schubert; Thomas Seidl; Arthur Zimek (2010). "On Using Class-Labels in Evaluation of Clusterings" (PDF). In Xiaoli Z. Fern; Ian Davidson; Jennifer Dy (eds.). MultiClust: Discovering, Summarizing, and Using Multiple Clusterings. ACM SIGKDD.
- ^ Gorban, A.N.; Sumner, N.R.; Zinovyev, A.Y. (2007). “Topological grammars for data approximation”. Applied Mathematics Letters 20 (4): 382-386.
外部リンク
[編集]- Fisher's Iris Data - UCI Machine Learning Repository: Iris Data Set sitory: Iris Data Set (Contains two errors which are documented)
