独立集合
この記事は英語版の対応するページを翻訳することにより充実させることができます。(2024年5月) 翻訳前に重要な指示を読むには右にある[表示]をクリックしてください。
|
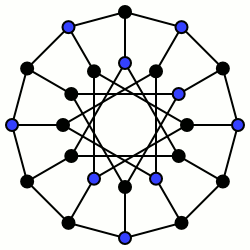
グラフ理論における独立集合(どくりつしゅうごう、英: independent set)または安定集合(英: stable set)は、1つのグラフ内で互いに隣接していない頂点の集合である。すなわち、頂点の集合 V で、V の任意の2つの頂点をつなぐ辺が存在しない場合をいう。等価的に、そのグラフの各辺の高々一方の端点のみが V の元である。独立集合の大きさとはその中の頂点の個数である。
極大独立集合 (maximal independent set) とは、任意の他の頂点を追加するとその集合に辺の両端点が含まれてしまうような独立集合である。
最大独立集合 (maximum independent set) は与えられたグラフ G の最も大きな独立集合であり、その大きさを α(G) と表記する[1]。このような集合を求める問題を最大独立集合問題と呼び、NP完全問題である。したがって、グラフの最大独立集合を求める効率的なアルゴリズムは存在が疑わしい。
与えられたグラフが特定の大きさの独立集合を持つかどうかを判定する問題を独立集合問題と呼ぶ。これは計算上、そのグラフが特定の大きさのクリークを持つかどうかの判定と等価である。このことは、グラフが大きさ k の独立集合を持つとき、その補グラフ(頂点は同じだが、辺が相補的なグラフ)は大きさ k のクリークを持つという事実から導かれる。独立集合(およびクリーク)の決定問題は、NP完全問題であることが知られている。
最大独立集合と極大独立集合は異なる概念である。極大独立集合は他のもっと大きな独立集合の部分集合とはならない。極大独立集合を求める問題は簡単な貪欲法で多項式時間で解くことができる。
特性
[編集]他のグラフ関連パラメータとの関係
[編集]ある集合が独立であるとは、そのグラフの補グラフのクリークと同値であり、2つの概念は相補的である。実際、十分大きなグラフで大きなクリークがない場合、独立集合は大きくなる。このあたりはラムゼー理論の主要研究テーマである。
ある集合が独立であるとき、その補集合は頂点被覆である。最大独立集合の大きさ α(G) と最小頂点被覆の大きさ β(G) の合計はそのグラフの頂点数となる。
2部グラフでは、最大独立集合の頂点数は最小辺被覆の辺数と等しい。
極大独立集合
[編集]他の独立集合の部分集合になっていない独立集合を「極大 (maximal)」であるという。そのような集合は支配集合 (dominating set) でもある。グラフは最大で 3n/3 個の極大独立集合を持つが、多くのグラフの極大独立集合の個数はそれより少ない。
n-頂点の閉路グラフでの極大独立集合の個数はペラン数列で与えられ、n-頂点の道での極大独立集合の個数はパドヴァン数列で与えられる[2]。したがって、どちらの個数もプラスチック数 1.324718 のべき乗と比例する。NP困難な問題を扱うアルゴリズムでは、極大独立集合をリストアップする処理をサブルーチンとして使うことが多い。
関連項目
[編集]- 辺独立集合をマッチングと呼ぶ。
脚注・出典
[編集]- ^ Godsil, Chris; Gordon Royle (2004) [1949]. Algebraic Graph Theory. New York: Springer. p. 3. ISBN 0-387-95220-9
- ^ Füredi, Z. (1987). “The number of maximal independent sets in connected graphs”. Journal of Graph Theory 11 (4): 463–470. doi:10.1002/jgt.3190110403.
