正軸体

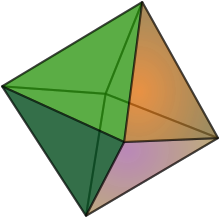
2次元正軸体（正方形）

3次元正軸体（正八面体）

4次元正軸体（正十六胞体）の投影図

正軸体（せいじくたい、cross-polytope）は、2次元の正方形、3次元の正八面体、4次元の正十六胞体を各次元に一般化した正多胞体。

なお、定義によっては形式的に0次元正軸体は点、1次元正軸体は線分となるが、正軸体一般の性質の一部が成り立たないため、0次元・1次元に正軸体は存在しないとすることが多い。

$\beta$体（ベータたい）ともいい、n 次元正軸体を $\beta _{n}$ と書く。

正単体、超立方体（正測体）と並んで、5次元以上での3種類の正多胞体の1つである。

作図

正軸体を作図するには、座標 $(\pm 1,0,0,\cdots ,0)$ の巡回

$(\pm 1,0,0,\cdots ,0),(0,\pm 1,0,\cdots ,0),\cdots ,(0,0,\cdots ,0,\pm 1)$

を頂点とし、最も近い（距離 ${\sqrt {2}}$ の）2点ずつを辺で結ぶ。最も近い3点ずつが面を構成し、m + 1 (0 ≤ m ≤ n - 1) 点ずつが m 次元面を構成する。

なおこの作図は、超立方体

$(\pm 1,\pm 1,\cdots ,\pm 1)$

の双対の作図と等価である。

またこうして作図された正軸体は、n 次元ユークリッド空間を $\mathbb {R} ^{n}$ で表して

$\{x\in \mathbb {R} ^{n}:\|x\|_{1}\leq 1\}$

でも定義できる。

性質

特にことわらない限り、辺の長さが a の n (≥ 2) 次元正軸体について述べる。

超体積は

${\frac {{\sqrt {2}}^{n}}{n!}}a^{n}$

超表面積は

${\frac {2^{n}{\sqrt {n}}}{(n-1)!{\sqrt {2^{n-1}}}}}a^{n-1}$

である。

ファセット（n - 1 次元面）は n - 1 次元正単体である。したがって一般に、 m (0 ≤ m ≤ n - 1) 次元面は m 次元正単体である。例えば正十六胞体（4次元正軸体）の面（2次元面）は正三角形（2次元正単体）、胞（3次元面）は正四面体（3次元正単体）である。また m 次元面の超体積は、正単体の超体積の公式より、

${\frac {\sqrt {m+1}}{m!{\sqrt {2^{m}}}}}a^{m}$

である。

対角線の長さは、作図法より

${\sqrt {2}}a\,$

で、全て直交する。

m (0 ≤ m ≤ n - 1) 次元面の個数は

$2^{m+1}{}_{n}\operatorname {C} _{m+1}$

である。これはパスカルのピラミッドの第 n + 1 段の三角形の第 m + 2 段の数字の総和に等しい。反対側のファセットの中心同士を結ぶ線に沿って見た場合、次元面たちは数字通りのグループに分割される。これは、$3^{n}=(1+2)^{n}$ を二項展開し、$3^{n}=(1+1+1)^{n}$ を三項展開することで示すことができる。特に、頂点（0次元面）は $2n$ 個、ファセットは $2^{n}$ 個である。${}_{n}\operatorname {C} _{m+1}$ はパスカルの三角形の第 n + 1 段の m + 2 番目の数字であり、n - 1 次元単体の m 次元面の個数である。

m (0 ≤ m ≤ n - 2) 次元面に集まるl (m + 1 ≤ l ≤ n - 1) 次元面の個数は

$2^{l-m}{}_{n-m-1}\operatorname {C} _{l-m}$

である。これはパスカルのピラミッドの第 n - m 段の三角形の第 l - m + 1 段の数字の総和に等しく、 n - m - 1 次元正軸体の l - m - 1 次元面の個数である。

双対は超立方体（正測体）である。