ピンホールカメラ

ピンホールカメラ(英: pinhole camera)は、写真レンズを使わない針穴(ピンホール)を利用したカメラである。針穴写真機ともいう。
構造が簡単で容易に製作できるため、理科の教材や工作の題材としてもよく使われ、また、夏休みの工作の題材としては、時期的に撮影対象として適した明るくかつコントラストが強い被写体を得やすいという利点もある。
概要
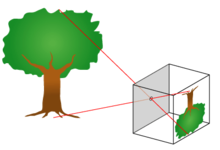
[編集]被写体の各点において乱反射(散乱)した光のうち、ピンホールの1点に到達する光線のみを通すことで、像面に被写体の像を得るという、最も単純なカメラの方式であり、実用的なレンズの開発以前からあったカメラである、初期のカメラ・オブスキュラの原理と全く同じものである。
このカメラを簡単に作るには、箱(遮光が目的なので、光を透さない材料で余計な孔などが無いことが必要。暗箱)の一面の中央にピンホールを開ければよい。箱の反対面に、トレーシングペーパーなどを張った窓を作れば直接観察できる。ただし得られる像が、レンズの場合と比べてかなり暗いので、最低でも簡単なバイザ風のフード、できれば大型カメラでピントグラスの確認の際に使うような被り布(冠布)があるとなお良い。理想としては箱の内側は反射防止加工をし、内部反射を抑えることが望ましい。
写真機として写真を得るには、写真フィルム等の感光材料や撮像素子などを置いて像を得る。しかしやはり像が暗いため、露光時間を十分にとる必要があり、三脚などしっかりと固定する手段を考える必要があるのが、レンズによって高速なシャッター速度が得られるカメラの工作との違いである。
インスタントカメラ用の感光材料(いわゆるインスタントフィルム)を使うと、その場で結果が得られるので露出時間を加減しての撮り直しもでき便利である。特に、従来のピールアパート方式のインスタントフィルムは照射面側に像が得られるため反転させる必要があったが、富士フイルムのinstax(いわゆる「チェキ」)は裏面照射なのでそのままで像が得られる。伝統的な写真材料としては印画紙を使うのだが、その場合、ネガの反転像が得られるので、密着焼き(コンタクトプリント)の要領で再度反転しネガを得れば、正立したポジ像となる。
レンズ交換式一眼レフなど、レンズ交換式のカメラがあれば、レンズ代わりの蓋に使うボディキャップを加工するなどすると簡単である。
(レンズによる)集光によって像を作るのではないため、通常のカメラにおいてレンズの焦点に関して議論されるようなパラメータは基本的には無い。しかし、画角などについては焦点距離と全く同じである。すなわち、写真レンズの議論における理想的な無限に薄いレンズの中央がピンホールの位置であり、ピンホールからフィルム面までの距離が焦点距離に相当する。なお後述するが、理想的なピンホール径に関して被写体までの距離への依存性があるため、その点ではピンホール写真にもピントがあるが、実際の写真ではまずわかるようなものではない[1]。
はっきりした像を得るためには、ピンホールの大きさは、一般にかなり小さくする必要があり(普通の大きさのカメラでは 0.数mm 程度、詳細は後述)、像が暗いため通常のカメラと比較して非常に長い露出時間を必要とする。典型的露出時間は、1秒から数時間、場合によっては1日くらいまでも露出することがある(これは、フィルムではなく印画紙を直接使う場合には、像が大きいことで面積あたりの光量が下がるのに加え、印画紙の感度がフィルムと比べて数段低めだという理由もある)。あるいは大光量のフラッシュを使うといった技法もある。
ピンホール径
[編集]この節には独自研究が含まれているおそれがあります。 |
波動光学により、理想的な(径が無限に小さい)点状のピンホールであっても、それを通った光が作る像は点ではなく、光線の回折によりエアリーディスクになる。そのため、ピンホールカメラをはじめ各種の光学系では、理想的な場合でも解像度に限界がある。顕微鏡などの性能の検討においては各種の理論式があるが(分解能の記事を参照)、ここではピンホールカメラの工作の目安程度として議論する。なお前述のようにピンホールカメラでは、その画角についてピンホールからフィルム面までの距離が、レンズを使った場合の焦点距離に相当するので、以下では便宜上その距離を「焦点距離」と呼ぶことにする。
被写体は無限遠であるとし、光の波長を λ、ピンホールの半径を r、焦点距離を b とすると、
の関係にあるとき、最も鮮明な画像となる(この議論では省いているが、係数が存在するはずでその値については議論があると思われる。本当に理想的なピンホール径を実際に求めるのであれば、実験的に行うことになろう。しかし、ピンホール径と「焦点距離」の間には、このような2乗(逆側から見ると平方根)に比例するという関係がある、という点については確かと見てよい)。
次に、近距離の被写体に対しては、以下の公式となる。この公式での、「c」は、焦点距離、「u」は、ピンホールから被写体までの距離、とする。
λを400nmとすると(これはかなり短い。理論的には、視覚に与える影響が大きいとされ、両端である赤と紫の中間である緑の波長で計算することも考えられる)、ピンホールの直径(mm) - 焦点距離の長さ(mm) は、0.2 - 25、0.3 - 56、0.4 - 100、0.5 - 156、0.6 - 225、0.7 - 306、0.8 - 400、0.9 - 506、1.0 - 625となる。
さらに前述のような、ピンホール径と「焦点距離」の関係があることから、次のような議論が成り立つ。幾何的に、イメージサークルの径は焦点距離に比例する。一方で理想的なピンホールの径は焦点距離の平方根に比例するのであるから、ピンホールの径が理想的であるとすると、
- より大きなカメラで大きな像を得ようとするほど、像は暗くなるが解像度は上がる
- 小さなカメラで小さな像を得た場合、(撮像素子の解像度は相応程度には高い必要はあるが)像の解像度は下がるが明るい像が得られる
というトレードオフがある(得た像の引伸しは理想的にできるものとする)。前者の理由により、作品づくりを探求するピンホール写真家はブローニー判やシートフィルムなど大きな感光材料を使うが、その場合(コストや取扱いの面倒さは置くとして)代償として長い露光時間か明るい被写体を必要とする。その逆が超小型ビデオカメラの類で、(ピンホールレンズ等と俗称しているものはレンズを併用しているが)NTSCでは走査線は525本であるなど解像度はたいして必要なく、撮像素子もフィルムカメラのイメージサイズに比べて極めて小さい一方、1コマあたりの露光時間が限られるため明るい像が必要なわけであるが、そういった条件にうまく一致する。詳細は注のリンク先を参照のこと[2]。
カメラを大型にした側の極北としては、太陽観測専用に、焦点距離4m・ピンホール直径2.6mmとした例が知られている[3]。
収差と口径食
[編集]レンズを使用しないため、パンフォーカス描写とレンズの特性に由来する収差が無いことはピンホールカメラの大きな魅力のひとつである。むろん絶対的に理想的なわけではなく、ピンホール径に由来する甘い像となることは不可避であるし、前述のように回折による限界もある。また、長い露光時間のために、静止した被写体でなければ「被写体ブレ」もある。
収差が無いという特性のため、かなりの広角まで樽型などの歪曲なしに撮影できることも魅力だが、原理的にコサイン4乗則による周辺光量低下は理論通りに発生するので限度がある。さらに、ピンホール周辺に厚みがあると、そのために一種の口径食のようにしてさらに周辺光量が低下する。そのため「ピンホールらしい」超広角撮影を狙う場合は、ピンホールの円の綺麗さだけではなく、周辺の厚みについても気を払う必要がある。


